- #1
venke
- 2
- 0
Hi,
I need to know for which nubers of x the serie is convergence.
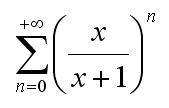
Is this possible whith d'Alombert? I have tried, but with no result.
Greets,
venke
I need to know for which nubers of x the serie is convergence.
Is this possible whith d'Alombert? I have tried, but with no result.
Greets,
venke