Force acting on a charge across a hybrid medium

[vcsharp2003]

Homework Statement

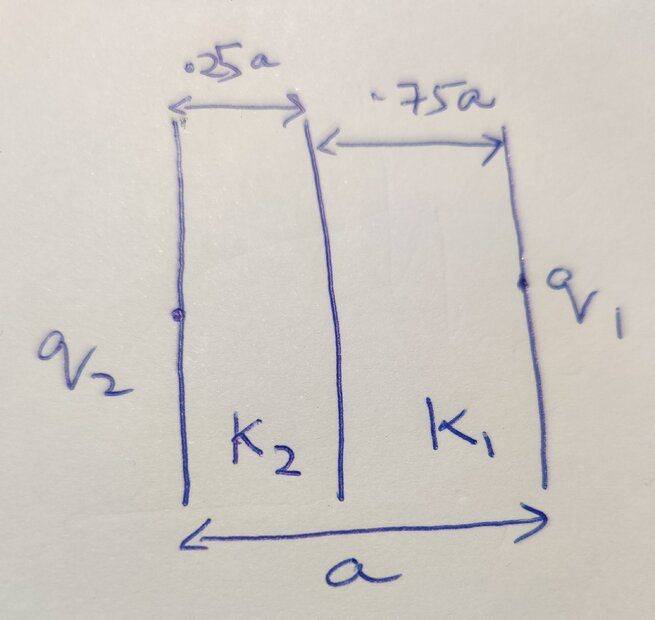
Two charge $q_1$ and $q_2$ are separated by two different dielectrics as shown in the diagram, having dielectric constants of $K_1$ and $K_2$. The two charges are separated by a distance $a$. What would be the force on charge $q_2$ due to charge $q_1$?

Relevant Equations

$F = \dfrac {kq_1q_2} {Kr^2}$, where k is Coulomb's constant and K is dielectric constant, F is force of attraction between the two charges $q_1$ and $q_2$ that are separated by a distance $r$

$E = \dfrac {kq} {Kr^2}$, where E is electric field due to a charge $q$ at a distance $r$ in medium having a dielectric constant $K$

The force on charge $q_2$ will depend on the electric field in medium with dielectric $K_2$.

Electric field in this second dielectric due to $q_1$ is $E = \dfrac {kq_1} {K_2r^2}$ where r would be the distance from $q_1$.
So, the electric field at the point where charge $q_2$ is there would be $E = \dfrac {kq_1} {K_2a^2}$

Therefore, force on second charge due to first charge would $F_{21} = \dfrac {kq_1q_2} {K_2a^2}$.

 

[kuruman]

Your answer would be correct if the entire distance $a$ had dielectric $K_2$. The electric field at the boundary between dielectrics is $\dfrac{kq_1}{K_1(\frac{3}{4}a)^2}$. What happens to it when you cross that boundary? In other words, what is continuous across the boundary?

 

[vcsharp2003]

Your answer would be correct if the entire distance $a$ had dielectric $K_2$. The electric field at the boundary between dielectrics is $\dfrac{kq_1}{K_1(\frac{3}{4}a)^2}$. What happens to it when you cross that boundary? In other words, what is continuous across the boundary?

Thankyou for the answer.

My understanding is that the electric field in a medium becomes $\dfrac {1} {K}$ times the electric field without any medium i.e. when there is vacuum, and I based my answer on this fact.

When the boundary of dielectrics is crossed from $K_1$ to $K_2$ then the electric field is still there except now it has a different formula i.e. a different strength, so electric field strength should not be a continuous function.