Force between charged Ring and Rod, disproved Newtons 3rd law?

[Hamiltonian]

Homework Statement

A system consists of a thin charged wire ring of radius $R$ and a very long uniformly charged rod oriented along the axis of the ring, with one of its coinciding with the centre of the ring. the total charge of the ring is equal to $q$. The charge of the rod(per unit length) is equal to $\lambda$. Find the interaction force between the ring and the rod

Relevant Equations

$\vec F = q\vec E$

This is the initial setup of the problem:

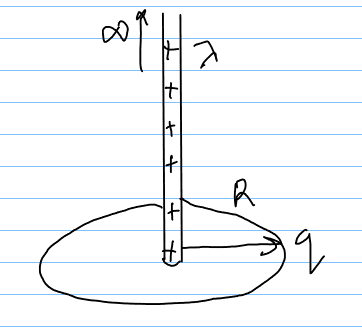
The electric field due to the ring is:
$$E = \int\frac{k(dq)}{(\sqrt{R^2 + x^2})^2}\frac{x}{\sqrt{R^2 + x^2}} = \frac{kqx}{(R^2 + x^2)^{3/2}}$$
the force on the rod due to this Electric field produced by the ring is:
Consider a differential element $dq$ of the rod on which the force is:

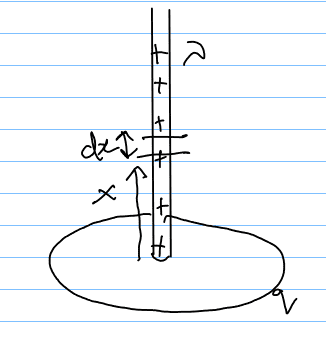
$$dF = E(dq) = E\lambda(dx)\frac{kqx\lambda(dx)}{(x^2 + R^2)^{3/2}}$$
The total force on the rod by the ring will be:
$$F = kq\lambda\int_{0}^{\infty}\frac{x}{(x^2 + R^2)^{3/2}} dx = -kq\lambda\left[\frac{1}{\sqrt{x^2 + R^2}}\right]_{0}^{\infty}=\frac{kq\lambda}{R} = \frac{q\lambda}{4\pi\epsilon_0 R}$$
this is the correct answer given in the book. But if we calculate the field due to rod on the ring and then calculate the Force acting on the ring, by Newtons 3rd law we should get the same force

calculating the field due to the rod:

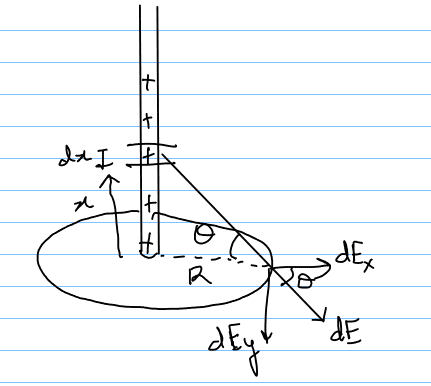
$$|d\vec E| = \frac{k(dq)}{(x^2+R^2)}$$
$$d\vec E = dE_x\hat i + dE_y\hat j$$
$$dE_x = dEcos\theta = \frac{k(dq)}{(x^2 + R^2)}\frac{R}{\sqrt{R^2 + x^2}} = \frac{k\lambda(dx)R}{(R^2+x^2)^{3/2}}$$
$$E_x = k\lambda R\int_{0}^{\infty}\frac{dx}{(R^2 + x^2)^{3/2}}=\frac{k\lambda}{R} = \frac{\lambda}{4\pi\epsilon_0R}$$
$$dE_y = dEsin\theta = k\lambda \frac{x(dx)}{(R^2 + x^2)^{3/2}}$$
$$E_y = k\lambda \int_{0}^{\infty}\frac{x}{(R^2 + x^2)^{3/2}}dx = \frac{k\lambda}{R} = \frac{\lambda}{4\pi\epsilon_0 R}$$

$$\vec E = \frac{\lambda}{4\pi\epsilon_0 R}\hat i + \frac{\lambda}{4\pi\epsilon_0 R}\hat j$$
$$|\vec E| = \frac{\sqrt{2}\lambda}{4\pi\epsilon_0R}$$
The force on the ring due to the field produced by thr rod is hence:
$$F = qE = \frac{\sqrt{2}q\lambda}{4\pi\epsilon_0R}$$
so if my math is correct I just disproved Newtons 3rd law I did the integrals twice by hand and once using wolfram alpha but still haven't been able to catch the error. Can someone help me out. I really hope there is a mistake in the math and not something conceptually wrong.

 

[kuruman]

Your second drawing is confusing. You have $dE_x$ pointing radially out and then element $dx$ along the wire perpendicular to $dE_x$. Be consistent. That may be your problem because the component of the electric field in the plane of the ring must integrate to zero by symmetry.

 

[Hamiltonian]

Your second drawing is confusing. You have $dE_x$ pointing radially out and then element $dx$ along the wire perpendicular to $dE_x$. Be consistent. That may be your problem because the component of the electric field in the plane of the ring must integrate to zero by symmetry.

The net electric field in the plane of the ring will have both a x and y component because the rod is not infinitely long in both direction, the bottom of the rod is at the center of the ring and the other end tends to infinity(in the +y direction).
Edit: I think I understand where I went wrong thanks a lot! the net force acting on the ring will only be in the y-direction and the x-componet gets canceled out due to the circular symmetry. all that time spent over nothing

 

[PeroK]

$$E_y = k\lambda \int_{0}^{\infty}\frac{x}{(R^2 + x^2)^{3/2}}dx = \frac{k\lambda}{R} = \frac{\lambda}{4\pi\epsilon_0 R}$$

Everything looks good up until here, although this should be $E_x$ according to your diagram. The only force is in the $x$ direction, as the force in the radial direction cancels out around the ring.