Force components for mass attached to two springs

[giraffe714]

Homework Statement

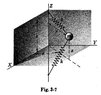
The particle of mass m, shown in Fig. 3-7 below, is free to move to any position under the action of the two identical springs. When m is in equilibrium at the origin of the coordinate axes, the length S of either spring is greater than the unstretched length l_0.
Show that $F_\phi = 0$.
Show that, for very small displacements from equilibrium, $$F_x = -2k(1 - \frac{l_0}{S})x, F_y = -2k(1 - \frac{l_0}{S})y, F_z = -2kz$$

Relevant Equations

$F = -\frac{\partial V}{\partial q}$, $V_{spring} = \frac{1}{2} kx^2$

So at first I tried to express the potential energy as a function of x, y and z, but since I'm not quite sure about the geometry of the situation, I decided to separate out the potential energy into three components: $V_x, V_y, V_z$ (I'm pretty sure this is valid because in the partial derivative with respect to one coordinate all the parts of the potential energy not related to that coordinate will go to 0 as constants.)
I used the formula for the potential energy of a spring to get $V_x = 2 * \frac{1}{2} kx^2$ (2 out front because there's two springs.) But even after taking the derivative of that I didn't get anything in terms of the fraction of $l_0$ and $S$? What would that fraction even represent geometrically? I got $F_x = -2kx$, which interestingly enough would be the correct expression if I did this with the z coordinates, but the thing is with the z coordinates is that there's also the potential energy due to gravity to consider - mgz, so $V_z = 2 * \frac{1}{2} kz^2 + mgz$, but then the force becomes $F_z = -2kz - mg$?

And maybe setting up the equations of motion and then multiplying the expressions for $\ddot{x}, \ddot{y}, \ddot{z}$ by the mass (F = ma) would be easier, but I struggle to see how that'd be more correct? Plus, I'm not even sure how to derive an expression for the kinetic energy in this scenario.

As for showing that $F_\phi = 0$, I know I need to derive an expression for the potential energy in terms of $\phi$, but I'm not sure how to do that at all.

 

[haruspex]

Show that $F_\phi = 0$.

I assume is this just F as a magnitude. Seems obvious since no springs change length there.

I used the formula for the potential energy of a spring to get $V_x = 2 * \frac{1}{2} kx^2$ (

Don't get confused between x as a coordinate of the mass and x as a spring extension.
Where can the mass be if the spring anchored at (0,0,S) is relaxed?
If the mass is at (x,y,z), what is the extension of that spring?

there's also the potential energy due to gravity to consider -

Is there? Gravity is not mentioned.

 

[giraffe714]

I assume is this just F as a magnitude. Seems obvious since no springs change length there.

What do you mean by this? Why don't the springs change length when the mass is being displaced from equilibrium?

Where can the mass be if the spring anchored at (0,0,S) is relaxed?
If the mass is at (x,y,z), what is the extension of that spring?

It can be at any length $l_0$ from the spring if it is relaxed (and the second one doesn't break, but we're not given any condition for breaking so I'll just assume that's not a problem.) And if the mass is at (x, y, z) the spring's extension would be the (x, y, s - z) (I'm assuming that z is below s from the diagram) but I'm not sure how to reduce that to only one number?

Is there? Gravity is not mentioned.

True, I just thought there had to be some other term in $V_z$ to make sure the expressions F_x and F_y had a different form from F_z, but now I see from (x, y, s - z) that that (probably) won't be a problem.

So I guess now I'm supposed to express (x, y, s - z) in terms of $l_0$ somehow? Okay, so I know that $x = S - l_0$, so I guess I can try to do something with that.

$$ V_x = k(S - l_0)^2 = k(S^2 - 2l_0S + l_0^2) $$

(no 1/2 because there's two springs) But the thing is that this doesn't really depend on x directly? Like yeah I can write $V_x = k\Delta x^2$ but does that really get us anywhere if the final expression's supposed to have l_0 and S in it? Wait...

$$ F_x = -2kx = -2k(S - l_0) = -2k(\frac{S}{S} - \frac{l_0}{S})S = -2k(1 - \frac{l_0}{S})S = -2k(1 - \frac{l_0}{S})(x + l_0) $$

Which is very close but the S is outside the bracket instead of x? It's probably a maths thing at this point, but I can't figure out how to get that l_0 out of the expression?

 

[haruspex]

What do you mean by this? Why don't the springs change length when the mass is being displaced from equilibrium?

Changing theta, according to the diagram, is just a rotation of the system about the z axis. Neither spring changes length.

It can be at any length $l_0$ from the spring if it is relaxed (and the second one doesn't break, but we're not given any condition for breaking so I'll just assume that's not a problem.) And if the mass is at (x, y, z) the spring's extension would be the (x, y, s - z)

No, that's the position of the mass relative to the anchor point, almost. (Should be (x, y, z-S).) How far is it from the anchor point? So what is that spring's extension?

 

[giraffe714]

Changing theta, according to the diagram, is just a rotation of the system about the z axis. Neither spring changes length.

Oh, yea, that makes sense. So I don't even have to derive an expression for V in terms of $\phi$? That's a relief.

No, that's the position of the mass relative to the anchor point, almost. (Should be (x, y, z-S).) How far is it from the anchor point? So what is that spring's extension?

How far is it from the anchor point? Well it's a length z - S from the anchor point, because it's a distance z from the origin, and the origin is a distance S away from the spring at (0, 0, S). So then $\Delta z = z - S - l_0$? Since z - S is the already stretched length of the spring?

 

[haruspex]

How far is it from the anchor point? Well it's a length z - S from the anchor point, because it's a distance z from the origin,

No, if it is at position (x,y,z-S) relative to the anchor point then, according to Pythagoras, the distance is …?

 

[BvU]

Does this help ?

$\$

 

[giraffe714]

No, if it is at position (x,y,z-S) relative to the anchor point then, according to Pythagoras, the distance is …?

Ohh, well it'd be sqrt(x^2+y^2+(z - S)^2), right?

 

[giraffe714]

Does this help ?

View attachment 342316

$\$

What is that diagram trying to say exactly? That the x component of the force is along the x direction..?

 

[BvU]

What is that diagram trying to say exactly? That the x component of the force is along the x direction..?

That is usually the case with $x$ components ...

And since the exercise asks for such a component, I thought a picture that shows you in detail how to calculate it would be useful

$\$

 

[giraffe714]

That is usually the case with $x$ components ...

And since the exercise asks for such a component, I thought a picture that shows you in detail how to calculate it would be useful

$\$

ohh, so it's just trigonometry now right? yea... yea I think that makes sense, so then

$$ V = k*\sqrt(x^2+y^2+(z - S)^2) \Rightarrow F_x = -\frac{1}{2}k*2x = -kx $$
But that's even further from the expression we're trying to get?? Plus, how will I be able to get a general expression for the force F when we need to take a partial derivative with respect to a coordinate anyways?

 

[BvU]

I don't follow. You want $F_x$ , not V.

In the left pic you see $m$ at the origin. In the center picture you see $m$ at position x. Force $F$ is found with $F = k(L'- l_0)$ where $L'$ follows from Pythagoras. And the $x$-component is then minus $F$ times a cosine which is also easily seen in the picture at right.

Lower half omitted for clarity -- a 2 can be factored in once you have $F_x$ from one spring.

$\$

 

[giraffe714]

I don't follow. You want $F_x$ , not V.

In the left pic you see $m$ at the origin. In the center picture you see $m$ at position x. Force $F$ is found with $F = k(L'- l_0)$ where $L'$ follows from Pythagoras. And the $x$-component is then minus $F$ times a cosine which is also easily seen in the picture at right.

Lower half omitted for clarity -- a 2 can be factored in once you have $F_x$ from one spring.

$\$

Okay, yeah, that makes sense, so the $F_x = Fcosθ = 2k(\sqrt(x^2+y^2+(z - S)^2) - l_0)cos(arcsin(\frac{S}{\sqrt(x^2+y^2+(z - S)^2)}))$ but that... that seems like too much trigonometry to be correct, plus I don't think there's a trig identity that simplifies cos(arcsin(whatever))? Could be wrong though, trigonometry isn't my strong suite.

 

[BvU]

Okay, yeah, that makes sense, so the $F_x = F\cos\theta = 2k(\sqrt{x^2+y^2+(z - S)^2} - l_0)\cos(\arcsin(\frac{S}{\sqrt{x^2+y^2+(z - S)^2}}))$ but that... that seems like too much trigonometry to be correct, plus I don't think there's a trig identity that simplifies cos(arcsin(whatever))? Could be wrong though, trigonometry isn't my strong suite.

$\cos\theta$ is also equal to $x/L'$ ! And you want to stop using $\sqrt{x^2+y^2+(z - S)^2}$. Just vary x and leave the others 0.

 

[erobz]

Okay, yeah, that makes sense, so the $F_x = Fcosθ = 2k(\sqrt(x^2+y^2+(z - S)^2) - l_0)cos(arcsin(\frac{S}{\sqrt(x^2+y^2+(z - S)^2)}))$ but that... that seems like too much trigonometry to be correct, plus I don't think there's a trig identity that simplifies cos(arcsin(whatever))? Could be wrong though, trigonometry isn't my strong suit.

If you have the arcsin as some function ( reading the arc whose sine is …), you can express the cosine using those same variables using Pythagorean Theorem.

 

[haruspex]

Okay, yeah, that makes sense, so the $F_x = Fcosθ = 2k(\sqrt(x^2+y^2+(z - S)^2) - l_0)cos(arcsin(\frac{S}{\sqrt(x^2+y^2+(z - S)^2)}))$ but that... that seems like too much trigonometry to be correct, plus I don't think there's a trig identity that simplifies cos(arcsin(whatever))? Could be wrong though, trigonometry isn't my strong suite.

If $\theta=\arcsin(x)$ then $x=\sin(\theta)$ and $\cos(\arcsin(x))=\cos(\theta)=\sqrt{1-\sin^2(\theta)}=\sqrt{1-x^2}$.