Force components of hanging pith balls

[Hijaz Aslam]

Consider the pith balls in the diagram:

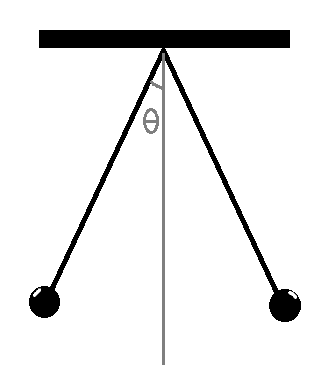
Both of them has mass 'm' and charge 'q'. The question asks for the charge on both the pith balls.

The concept is a bit straightforward. But I am confused at the force distribution experienced by the pith balls.
My text tackles the problem with reference to the following diagram.

And taking $Tcos\theta=g$ and then using $T=\frac{g}{cos\theta}$ and then proceeding to find the charge.

The part I am confused with is that, if we consider the following image

why can't we resolve the vectors as shown in the image and use $T=gcos\theta$ and proceed?

Is it because the tension has a component perpendicular to that of 'g' ?
I am confused with the Free Body Diagram of forces. Is there any good article available on web?

 

[Philip Wood]

Corrections to the forces you have shown on the left hand ball. (1) The downward force is mg. (2) You have omitted the horizontal force to the left exerted by the right hand ball due to the charges on the balls. If you include this force it's easy to see why T=(m)gcosθ is wrong. Say if you don't see this.

 

[Hijaz Aslam]

Corrections to the forces you have shown on the left hand ball. (1) The downward force is mg. (2) You have omitted the horizontal force to the left exerted by the right hand ball due to the charges on the balls. If you include this force it's easy to see why T=(m)gcosθ is wrong. Say if you don't see this.

Am sorry. My text gave the value of m=1. I missed out the 'm'.

I understand that there are two forces acting on both the balls due to each other. But are those forces a concern upon my doubt? Can you please explain?

 

[Philip Wood]

The right hand ball exerts a force equal to $\frac{Q^2}{4 \pi \epsilon_0 r^2}$ to the left on the left hand ball. This is the force you haven't shown. If you include it on your diagram things should become clearer. If they don't, do say. [The left hand ball exerts a force of the same magnitude, but to the right, on the right hand ball.]

 

[Hijaz Aslam]

Mr.Philip Wood, as I've commented above, I quite understand the role of the electrostatic force in play. I think I've got a satisfactory answer from my father. If we consider the image below. The mistake I made is that, I stated that the force $mgcos\theta$ is countered by the tension 'T'. But if we take the component of Tension along the y-axis we have $Tcos\theta=mgcos^2\theta < mg$. This implies that there's a net acceleration in the negative y-direction, which violates the condition of equilibrium.

If this explanation is wrong, please point it out.

 

[jtbell]

As Philip pointed out, a third force acts on the left-hand ball, namely the repulsive electrical force exerted by the charge on the right-hand ball. This force is exactly such that the vector sum of all three forces on the left-hand ball is zero.

 

[Philip Wood]

Clearly the two forces you have shown acting on the left hand ball can't be in equilibrium, as the tension has an unbalanced horizontal component. I'm surprised that you don't seem to want to include the third (electrostatic) force, which enables equilibrium to be achieved. This force (whose magnitude I'll call F) acts to the left so it is clear that
$T sin \theta = F$ and $T cos \theta = mg$.
It's as simple as this. If you divide one equation by the other you can eliminate T.
The reason why $T ≠mg cos \theta$ is simply that F (not just mg) has a (negative) component in the direction of T. That's why I kept urging you to show F on your diagram!

 

[Philip Wood]

So, resolving along the direction of the string: $T = mg cos \theta + F sin \theta$.
I've written this equation because it shows you why $T = mg cos \theta$ is wrong. I'm not recommending that you use this equation, as it's far easier to use the equations obtained by resolving horizontally and vertically, as given in my previous post. In fact it's easier still to draw a vector triangle showing the three forces adding to zero. Then it's immediately clear that $F = mg \ tan \theta$.

 

[Hijaz Aslam]

Oh yes. Mr.Philip Wood I am sorry about my ignorance. I misunderstood your solution. I get it now. Thanks

 

[Philip Wood]

I'm so pleased that you now understand.

Just an aside: I'm a little worried about your textbook. I hope it didn't really say m = 1, with no units. In any case it's better to work with algebraic symbols where possible, and put in values only near the end. This makes it easy to check for consistency of units (or dimensions) as you go, and usually saves time.

 

[Hijaz Aslam]

Just an aside: I'm a little worried about your textbook. I hope it didn't really say m = 1, with no units. In any case it's better to work with algebraic symbols where possible, and put in values only near the end. This makes it easy to check for consistency of units (or dimensions) as you go, and usually saves time.

It's not the fault with my textbook, I've made a mistake. I completely forgot the 'm' in the diagram. I am referring to The Fundamentals of Physics - Halliday/Resnick/Walker, but an edited version of it.