MatinSAR
- 673
- 204
- Homework Statement
- A certain force field is given to me and I should do the following tasks to find out is it a conservative field or not.
- Relevant Equations
- pls see below.
Picture of question:
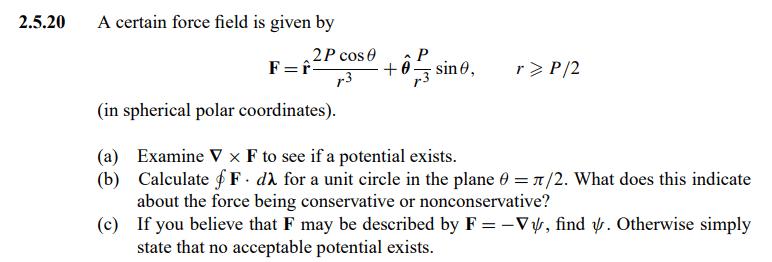
Part (a) : ##\nabla \times \vec F = 0## so a Potensial exists. I don't have problem with this part.
Part (b) : what I've done :
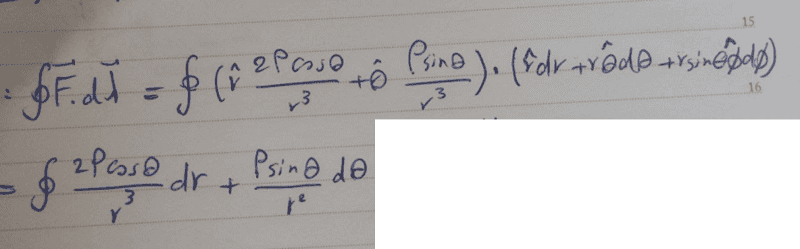
First experssion is 0 because ##\theta = \dfrac {\pi} {2}##. I don't know how to integrate over ##\theta ## when it is a constant.
Part (a) : ##\nabla \times \vec F = 0## so a Potensial exists. I don't have problem with this part.
Part (b) : what I've done :
First experssion is 0 because ##\theta = \dfrac {\pi} {2}##. I don't know how to integrate over ##\theta ## when it is a constant.