Force Generated By Leg Muscles in Free Body Diagrams

[annamal]

TL;DR Summary

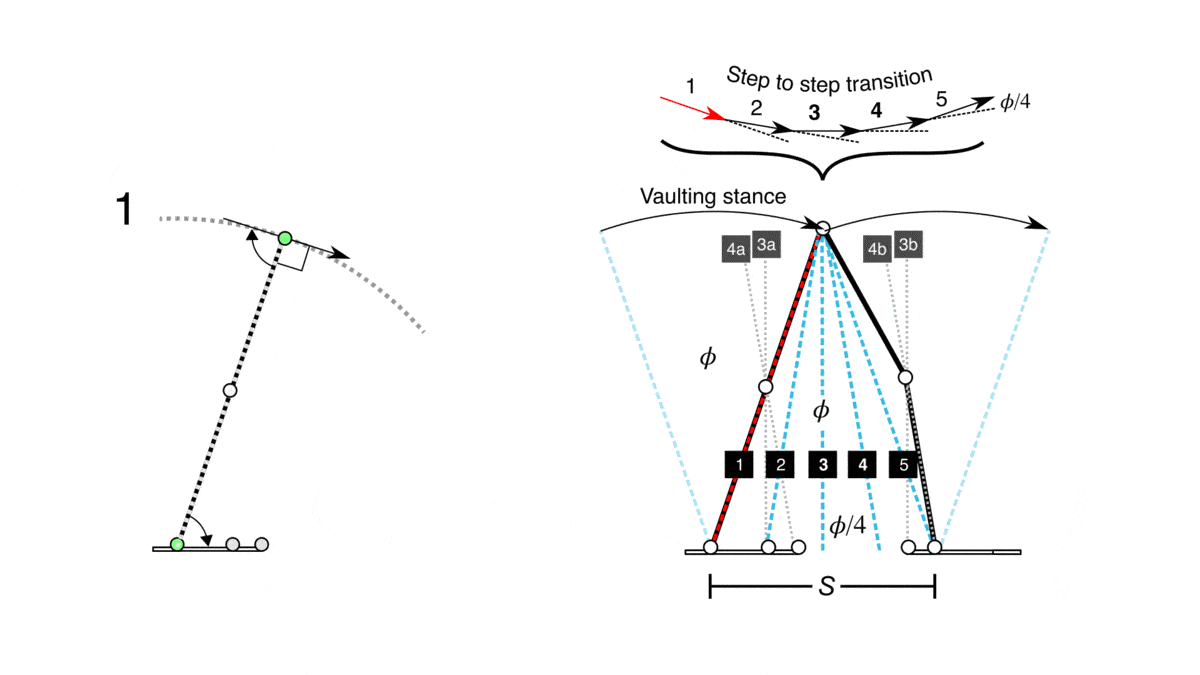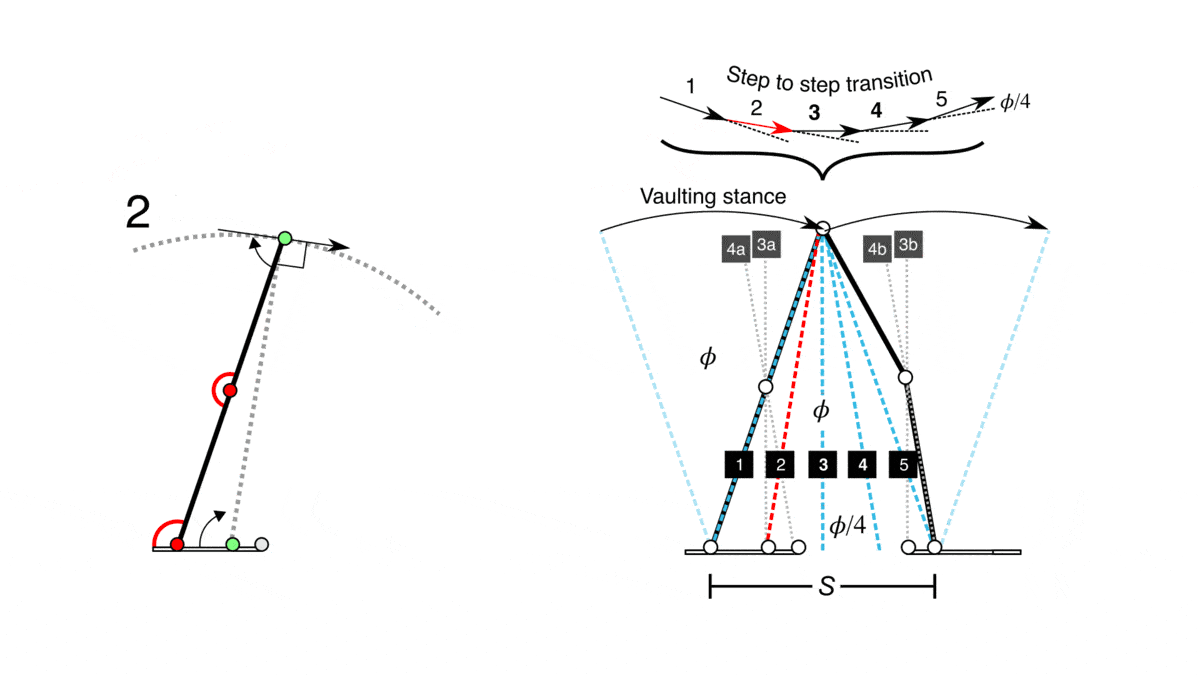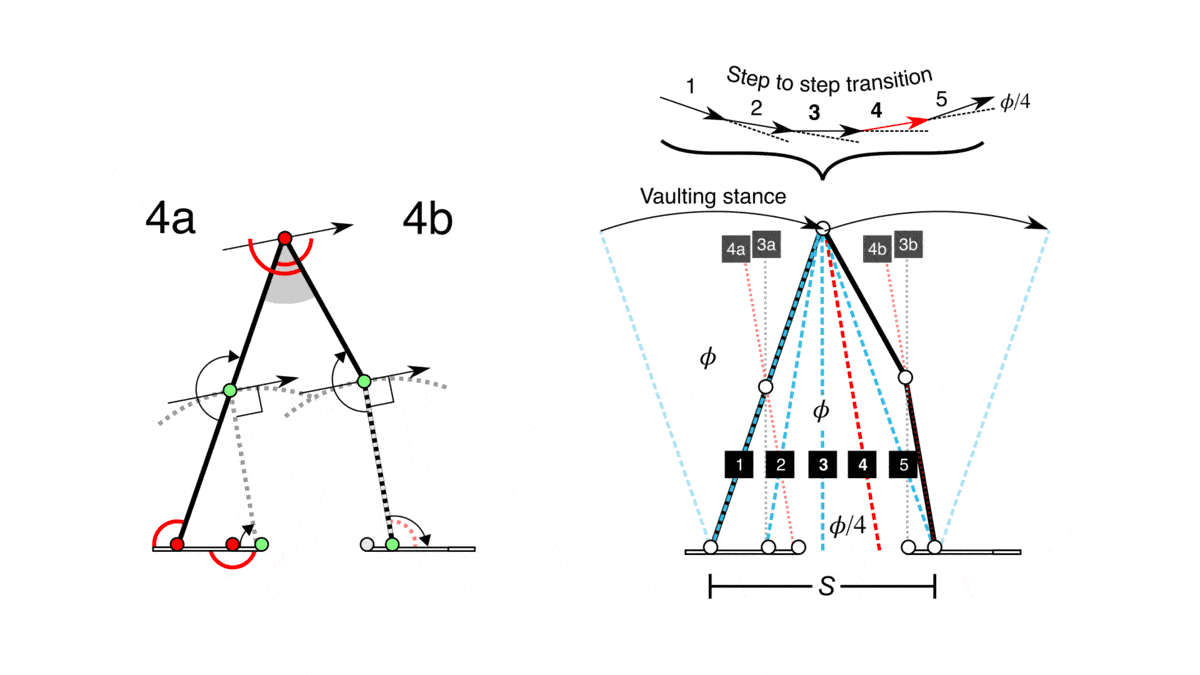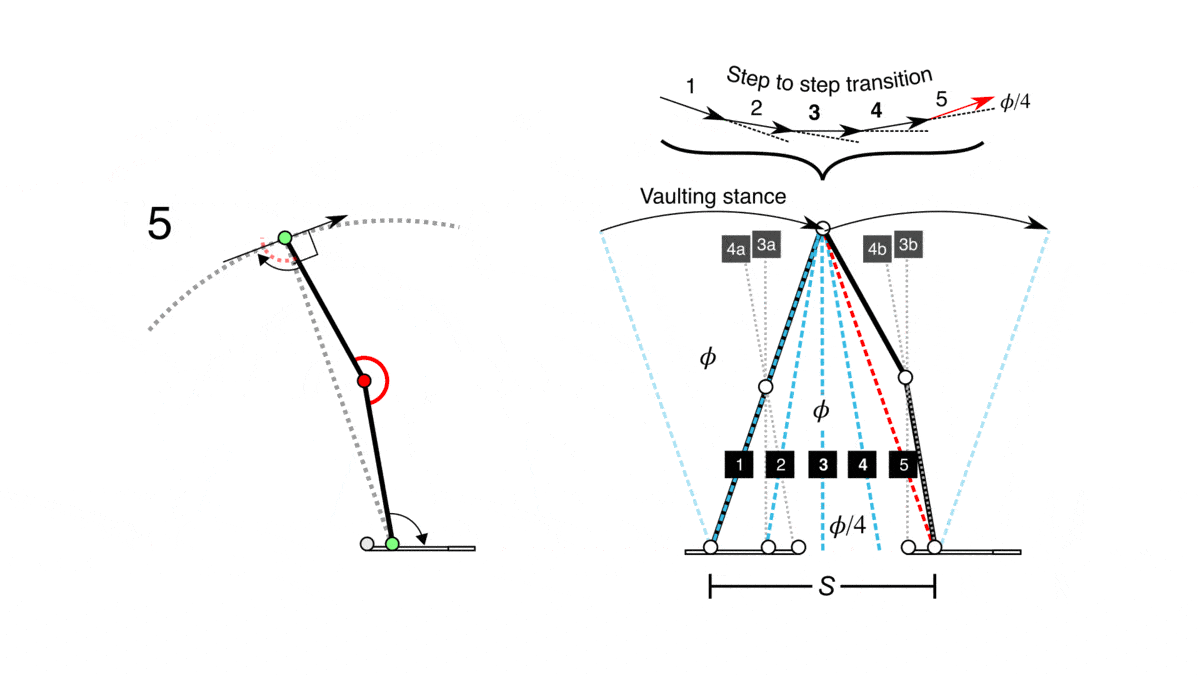
Suppose a person is walking on the ground without slipping. For the free body diagram of just the person, only the frictional force is drawn in the horizontal direction. The force exerted by the leg muscles to generate a force against the ground is considered an internal force. What would be the equal and opposite force of the force generated by the leg muscles since that force is an internal force of the free body diagram of the person?

Suppose a person is walking on the ground without slipping. For the free body diagram of just the person, only the frictional force is drawn in the horizontal direction. The force exerted by the leg muscles to generate a force against the ground is considered an internal force. What would be the equal and opposite forces of the force generated by the leg muscles since that force is an internal force of the free body diagram of the person?

 

[hutchphd]

1. The force of the leg muscle onto the foot is an internal force and not of interest.
2. The force of the foot onto the ground is a force onto the ground and not directly of interest.
3. The reaction force of the ground on foot is of interest and is exactly equal and opposite the force (2) above

 

[annamal]

1. The force of the leg muscle onto the foot is an internal force and not of interest.
2. The force of the foot onto the ground is a force onto the ground and not directly of interest.
3. The reaction force of the ground on foot is of interest and is exactly equal and opposite the force (2) above

Ok, so I guess I am asking what force causes the force of the leg muscle onto the foot and since it is an internal force, what is the reaction force to that force?

 

[hutchphd]

It is the force of the foot on the muscle (also an internal force and again probably not of interest). The reaction force of A on B is always the force of B on A. Always. $$\vec F_{AB}=- \vec F_{BA}$$

 

[A.T.]

Ok, so I guess I am asking what force causes the force of the leg muscle onto the foot and since it is an internal force, what is the reaction force to that force?

Additionally to what @hutchphd wrote: Causation plays no role in Newton's 3rd Law. It is arbitrary which of the two forces you consider reaction and which action.

 

[Lnewqban]

What would be the equal and opposite force of the force generated by the leg muscles since that force is an internal force of the free body diagram of the person?

Would that be the inertia of the body to be moved forward plus the changes in potential energy of the center of mass?
Walking uphill, for example, requires greater muscular work and higher friction force of the foot against the slope than walking on a flat surface.

The internal forces come from contractions of certain muscles, which form a triangle respect to two bones.
Those internal forces induce a moment in the leg simultaneously with a moment in the upper body to fall forward, completing one balanced step.

Please, see:
https://en.wikipedia.org/wiki/Leg_mechanism

https://vondesmos.wordpress.com/2016/07/19/a-walking-machine/

 

[A.T.]

What would be the equal and opposite force of the force generated by the leg muscles since that force is an internal force of the free body diagram of the person?

Would that be the inertia of the body to be moved forward plus the changes in potential energy of the center of mass?

If we are talking about equal and opposite force in the sense of Newton's 3rd Law, then no. Newton's 3rd Law is as trivial and simple as stated by @hutchphd in post #4. Also, neither "inertia of the body" nor "change in potential energy" are forces.

 

[vanhees71]

Well, by definition the potential's "change with position" is the "force" ;-)). Of course it's better to make precise statements in terms of math,
$$\vec{F}=-\vec{\nabla} V.$$

 

[TonyStewart]

https://vondesmos.wordpress.com/2016/07/19/a-walking-machine/

View attachment 325679

Would that be the inertia of the body to be moved forward plus the changes in potential energy of the center of mass?View attachment 325679
Nice "walking machine" but no resemblance to human walking.

The first various ligament actions pulled by muscles, first raise 1 heel to tilt while leaning the centre of mass forward, to scissor forward the alternate thigh and propel with the ball of the foot with the raised heel.