Force of one dipole on another; non-symmetric

[mhryciw]

Homework Statement

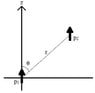
The dipole p₁ lies on the z axis at the origin. p₂ is at a distance r away . Using cylindrical coordinates, p₂ is at angle θ down from the z axis (see diagram), and points in the z direction. r is assumed to be much greater than d (distance between charged ends of dipole) therefore are evaluated as pure dipoles. I need to find the force of p₁ on p₂.
The question encourages us to refer back to the derivation of the formula: F=(p$\cdot$$\nabla$)E

Homework Equations

V=(p₁cosθ)/(4∏ε₀r²)
E_(r,θ)=-$\nabla$V_(r,θ)

The Attempt at a Solution

There is no dependence on ∅.
The E-field by the potential is:
E_(r,θ)=|p|/(4∏ε₀r³)(2cosθ$\hat{r}$+sinθ$\hat{θ}$)
I'm just unsure of how to solve this. Do I multiply the |p|/(4∏ε₀r³) component into the (2cosθ$\hat{r}$+sinθ$\hat{θ}$) and then take the gradient of that beast? Just point me in the right direction please! :)

 

[mark726]

it is important to approach problems in a systematic and logical manner. In this case, we are given the position and orientation of two dipoles and are asked to find the force between them. The first step would be to determine the electric potential at the location of p2 due to p1. This can be done using the given formula for the potential:

V=(p1cosθ)/(4∏ε0r2)

Next, we can use the definition of electric field to find the electric field at the location of p2:

E(r,θ)=-\nablaV(r,θ)

Since we are using cylindrical coordinates, we can express the electric field in terms of the unit vectors in the cylindrical basis:

E(r,θ)=E_r(r,θ)\hat{r}+E_θ(r,θ)\hat{θ}+E_z(r,θ)\hat{z}

Where E_r, E_θ, and E_z are the components of the electric field in the r, θ, and z directions respectively. We can use this expression to find the force on p2 due to p1 using the formula:

F=(p\cdot\nabla)E

Where p is the dipole moment of p2. This formula takes into account the orientation of the dipole and gives us the force in the direction of the dipole moment.

In summary, to find the force of p1 on p2, we need to first find the electric potential at the location of p2 due to p1, then use the definition of electric field to find the components of the electric field, and finally use the formula for force to find the force in the direction of the dipole moment. I hope this helps guide you in the right direction.