Force of pressurized water exiting a hose or pipe?

[RobertGC]

TL;DR Summary

Two different methods of calculating appears to give different answers.

Well known examples of the force produced by pressurized water exiting a pipe:

JetLev Water Propeled jet Pack.
Hovering Car.
I need to calculate the maximum for the thrust produced when the hose or pipe is bent rearward.

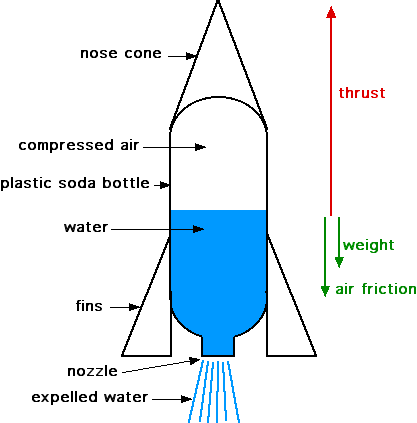
Since this is similar to the case of a water bottle rocket, the guess is it should be the same as that case:

The thrust force is:

F = 2*(P - P₀)*A_n,

Where P is the pressure in the pipe, P₀ is the ambient air pressure, and A_n is the area of the nozzle.

https://www.ohio.edu/mechanical/thermo/property_tables/gas/adiabatic/rocket/rocket.html

Note the extra factor of 2 there. An odd aspect of this formula is that it would appear that you could just increase the thrust by making the nozzle size larger.

However, note in the derivation you need the cross-sectional area to be small enough on exit so that, by the Bernoulli principle, the exit velocity would be large. So making the exit area larger would obviate the argument used.

Here is the issue though. Another formula used for calculating the force required to hold a pipe in place because of the force produced on the bend due to the momentum of the water flow may, or may not, give a different answer.

See the calculations here:

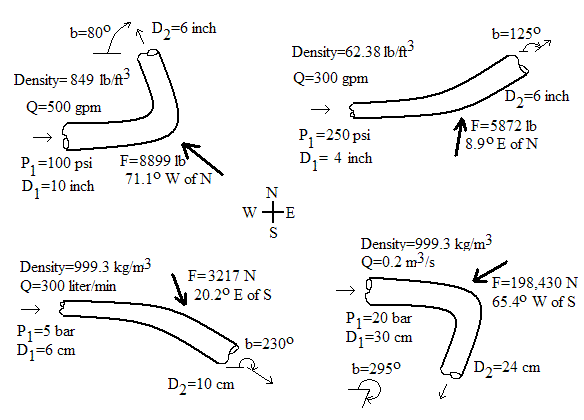
Equations for force on pipe bend calculation
The equations used in our calculation can be found in nearly any college level fluid mechanics textbook (e.g. Munson et al., 1998) or fluid mechanics reference handbook. The force equations are based on linear momentum conservation. P₂ is computed using the Bernoulli Equation, which assumes negligible friction loss around the bend.
Subscript 1 is upstream of bend; Subscript 2 is downstream of bend; Subscript x is x-component of force; Subscript y is y-component of force. For a pipe bend in the horizontal plane where friction effects around the bend are negligible:
Fx = -P₁A₁- P₂A₂ cos(b) - d Q [V₁ + V₂ cos(b)]
Fy = P₂A₂ sin(b) + d V₂ Q sin(b) F = (Fx² + Fy²)^1/2
Q=VA, A=π D² / 4
P₂ = P₁ + d (V₁² - V₂²) / 2
Variables
To use the equations above, a consistent set of units must be used. The variables below show the SI (System International) units for each variable. Our calculation allows a variety of other units with the conversions made internally within the program.
A=Pipe flow area (m²)
b=Pipe angle shown in the figure above (valid range is 0 to 2π radians or 0 to 360^o)
d=Liquid (or gas) mass density (kg/m³)
D=Pipe diameter (m)
F=Resistive (reaction) force (N)
P=Gauge pressure (N/m², relative to atmospheric pressure_
https://www.lmnoeng.com/Force/ForceBend.php

For the scenario we are considering, the hose is bent backwards, so the angle b in the formula is 0. So,

Fx = -P₁A₁ - P₂A₂ - d Q [V₁ + V₂]
Fy = 0

The minus sign is because the formula is calculating the force required to oppose the force on the pipe. Let’s look at the case, where the cross-sectional area is not changed. Then, it would appear, P₁ = P₂, and A₁ = A₂, V₁ = V₂. Then Fx = - 2PA - 2dQV.

For the scenario we are considering the pressure is high, but the speed V of the flow is low. Then the calculated force would be approx. Fx = -2PA, i.e., the force by the water on the pipe is Fx = 2PA.

The problem is this would be much larger than the water rocket formula since it uses the full cross-sectional area of the pipe, not just that of the nozzle.

Perhaps the problem is for the formula to be correctly applied what should be done is is for the exit pressure P₂ we should use the pressure of the ambient air, much smaller than the initial pressure in the pipe of P1. In that case the P₂A₂ term is approx. 0, so can be neglected. But what should we take for V₂?

By the Bernoulli formula for P₂ being greatly reduced that should ramp up the velocity V₂. Then V₂ would be much larger than V₁ and we can neglect dQV₁, so Fx = -P₁A₁ - dQV₂. We still have that force being much larger than the water bottle rocket case because A₁ is the area of the full hose/pipe not that of a nozzle.

So what is the real force being produced? This is something that can be tested for pressure washers. You would bend the hose backwards, and measure the force on the hose tending to force the hose away from you.

Pressure washers are provided with various nozzle sizes. The force produced should also be measured for all the nozzles provided as well as for the case with no nozzle.

Robert Clark

 

[RobertGC]

That link I gave has a calculator for the force on a pipe bend. However, it is a for pay calculator. This page has a free one:

https://www.engineeringtoolbox.com/forces-pipe-bends-d_968.html

The answer is far above that you get for ”water bottle rocket” method. That’s why I wanted to see what people actually got when they tested it on a pressure washer.

Robert Clark

 

[Chestermiller]

You do realize that there is a fundamental difference between the water rocket situation and the steady flow in a pipe bend situation, right? If so, please articulate your understanding..

The steady flow analyses you presented for the reaction force of the fluid on a pipe bend are all correct. So study them carefully so that you can reproduce them.

Please provide the details of the analysis for the water rocket.

 

[RobertGC]

The details of the water rocket analysis are given in the link cited:

https://www.ohio.edu/mechanical/thermo/property_tables/gas/adiabatic/rocket/rocket.html

The primary difference between the water bottle rocket and the pipe bend scenario is that for the pipe bend the water continues inside the pipe, perhaps for some distance.

But how long is that distance for the water bottle rocket scenario to hold sway?

Robert Clark

 

[Chestermiller]

The details of the water rocket analysis are given in the link cited:

https://www.ohio.edu/mechanical/thermo/property_tables/gas/adiabatic/rocket/rocket.html

The primary difference between the water bottle rocket and the pipe bend scenario is that for the pipe bend the water continues inside the pipe, perhaps for some distance.

But how long is that distance for the water bottle rocket scenario to hold sway?

Robert Clark

The water rocket analysis breaks down when the exit area becomes large because the Bernoulli assumption of negligible upstream velocity (compared to the exit velocity) becomes no longer valid. The rocket analysis is only valid if the ratio of the areas is small.

I might also mention that the thrust force on the rocket body is not coming from the exit area momentum of the water stream; it is coming mainly from the internal gas pressure force on the rocket body which is no longer partially balanced by the pressure force at the exit. The exit momentum of the water stream is just the net of the pressure forces on the rocket body which are what really combine to determine its acceleration. This is analogous to the unbalanced pressure forces acting on the pipe bend.

 

[RobertGC]

Here is the water bottle rocket analysis:

We’ll use the first equation shown there which amounts to F = (mass flow rate)*(exit velocity). Take for example this pressure washer:

PowerShot PS4240 4200 PSI at 4.0 GPM Cold Water Gas Pressure Washer with HONDA GX390.
https://www.homedepot.com/p/SIMPSON...her-with-HONDA-GX390-49-State-60456/203448619

It can do 4,200 PSI at 4 GPM with a hose at 3/8 inch inner diameter. We’ll convert to metric to have consistent units. A gallon is 3.78 liters so 4 GPM, is 15.12 liters per minute which for water means 15.12 kg per minute or 0.25 kg/s.

For the exit speed, we’ll use the last formula given there,

(P - P_a)/ρ_w = u_ex²/2.

Now 4,200 is 4,200/14.7 = 286 bar = 286E5 Pascals.

Then u_ex² = 2*286E5/1000 = 57,000, and u_ex = 240 m/s.

So the force would be 0.25 * 240 = 60 N, or 6 kg-force, about 12 pounds.

On the other hand, let’s see what the answer would be using the online calculator. Here we will not restrict the area like in the water bottle case. So the diameter will be 3/8” = 9.53E-3 m. We need to divide volume for rate of 0.25 liters per second by the area cross section to get the speed. This results in a speed of 3.5 m/s.

Plugging the numbers into the calculator here:

https://www.engineeringtoolbox.com/forces-pipe-bends-d_968.html

results in a force of 915 pounds!

Robert Clark

 

[Chestermiller]

Here is the water bottle rocket analysis:

View attachment 288875

We’ll use the first equation shown there which amounts to F = (mass flow rate)*(exit velocity). Take for example this pressure washer:

PowerShot PS4240 4200 PSI at 4.0 GPM Cold Water Gas Pressure Washer with HONDA GX390.
https://www.homedepot.com/p/SIMPSON...her-with-HONDA-GX390-49-State-60456/203448619

It can do 4,200 PSI at 4 GPM with a hose at 3/8 inch inner diameter. We’ll convert to metric to have consistent units. A gallon is 3.78 liters so 4 GPM, is 15.12 liters per minute which for water means 15.12 kg per minute or 0.25 kg/s.

For the exit speed, we’ll use the last formula given there,

(P - P_a)/ρ_w = u_ex²/2.

Now 4,200 is 4,200/14.7 = 286 bar = 286E5 Pascals.

Then u_ex² = 2*286E5/1000 = 57,000, and u_ex = 240 m/s.

So the force would be 0.25 * 240 = 60 N, or 6 kg-force, about 12 pounds.

On the other hand, let’s see what the answer would be using the online calculator. Here we will not restrict the area like in the water bottle case. So the diameter will be 3/8” = 9.53E-3 m. We need to divide volume for rate of 0.25 liters per second by the area cross section to get the speed. This results in a speed of 3.5 m/s.

Plugging the numbers into the calculator here:

https://www.engineeringtoolbox.com/forces-pipe-bends-d_968.html

results in a force of 915 pounds!

Robert Clark

I'm assuming you're doing a U with an internal pressure of 4200 psig. Most of the reaction force is due to the pressures on the fluid on the two ends of the U. These have to be offset by the reaction force. If you multiply the pressure by the area of the hose and then by 2, you get 927 lbs.

 

[Chestermiller]

The problem with your power shot analysis is that a 3/8" diameter for the nozzle outlet is not compatible with a 4200 psi pressure and a flow rate of 4 gpm. The diameter at the exit would have to be much less than this, on the order of, say 1/8".

 

[RobertGC]

The problem is this is an engineering analysis so it’s supposed to be representing what is happening for real world applications. Notice this huge force applies for any of the common pressure washers. Use the online calculator for any of the common pressure washers, you’ll get hundreds of pounds if the hose is bent around to face rearwards. This is why I wanted to see if it really is that high.

As you mentioned the key distinction is that for the water bottle scenario the exit towards the atmospheric air pressure is close to where the bend is and you restrict the nozzle size. Notice also if you don’t restrict the area with a nozzle, then the force of the exiting water is not just directed rearward. But because the pressure is so high in the hose, it would rapidly expand out in all directions when exiting. So the total force going in all directions might still be that high as indicated by the calculator, but it would not be felt as a force pushing directly rearward.

But suppose we don’t exit out to the air and don’t restrict to a smaller nozzle? Then the force on the bend really should be that high as indicated by the calculator. But as a practical matter how could we have a flow of water, without at some point, exiting out to the open air?

How about this as a brain teaser: suppose we take the hose and feed it back into the pump. Would the pump add an additional 4,200 psi pressure to the water already at 4,200 psi when it came in?

Robert Clark

 

[Chestermiller]

I have no idea what you are saying. If you want help analyzing a specific system with well-specified intervals, I’ll be glad to help.

 

[RobertGC]

So I finally broke down and paid for the for-pay online calculator at the link:
https://www.lmnoeng.com/Force/ForceBend.php

I was surprised to see when I did put in the restricted diameter hose dimension after the bend that the force was still much higher than the water bottle rocket case:

The force calculates out to be 477 pounds! This compared to the ca. 12 pounds you get from the water bottle rocket analysis.

Note the exit gauge pressure is approx. 0, i.e., relative to that of ambient air, and the flow speed is greatly increased. This now is a real discrepancy.

So which is the right answer?

Robert Clark

 

[Chestermiller]

So I finally broke down and paid for the for-pay online calculator at the link:
https://www.lmnoeng.com/Force/ForceBend.php

I was surprised to see when I did put in the restricted diameter hose dimension after the bend that the force was still much higher than the water bottle rocket case:

View attachment 288959

The force calculates out to be 477 pounds! This compared to the ca. 12 pounds you get from the water bottle rocket analysis.

Note the exit gauge pressure is approx. 0, i.e., relative to that of ambient air, and the flow speed is greatly increased. This now is a real discrepancy.

So which is the right answer?

Robert Clark

Both answers are correct. But you are not comparing equivalent situations and equivalent forces. The rocket is accelerating and the piping is not. Also, that 477 sounds way high. For a 1/8" nozzle, I get a force more like 100 lbs. If you want to compare equivalent forces, calculate the force the water exerts on the nozzle.

 

[RobertGC]

Both answers are correct. But you are not comparing equivalent situations and equivalent forces. The rocket is accelerating and the piping is not. Also, that 477 sounds way high. For a 1/8" nozzle, I get a force more like 100 lbs. If you want to compare equivalent forces, calculate the force the water exerts on the nozzle.

Keep in mind this calculates the force that would need to be supplied by a block placed against the hose or pipe to keep it in place. In other words, the hose or pipe would move if that restraining block was not there.

About the size of the hose, according to the calculator the size of the hose that would bring the exit pressure down to that of the ambient air, i.e., 0 gauge psi, is 0.04547”, about 1/22nd of an inch. Try the calculation of the force then.

Robert Clark

 

[Chestermiller]

Keep in mind this calculates the force that would need to be supplied by a block placed against the hose or pipe to keep it in place. In other words, the hose or pipe would move if that restraining block was not there.

You do realize that the hose is under tension, correct? And that the force exerted by the fluid on the nozzle is in the opposite direction of the fluid flow, correct?

About the size of the hose, according to the calculator the size of the hose that would bring the exit pressure down to that of the ambient air, i.e., 0 gauge psi, is 0.04547”, about 1/22nd of an inch. Try the calculation of the force then.

The exit pressure is always that of the ambient air (o psig).

Let's work on a focus problem to solidify your understanding (or, at least, to try to develop it). I have a straight 3/8" ID hose with a 3/8" ID nozzle attached, that tapers down to 1/8" ID at its exit (into the air). I am flowing water through the hose and nozzle at a volumetric flow rate of 4 gpm. What is the pressure in the hose upstream of the nozzle, and what is the force (and in what direction) that the flowing water exerts on the nozzle? What is the tension or compression force in the hose?

Robert Clark

 

[Chestermiller]

To improve your confidence in my fluid mechanics expertise, see post #4 in this thread: https://www.physicsforums.com/threa...ith-compressible-fluids.1006984/#post-6540450

 

[RobertGC]

I have no doubt you are quite knowledgeable in the topic. And actually I will want to ask another question that the link you gave discusses, this time in compressible flow. I’d like to get your feedback on that as well. I’ll get to that in a day or so.

But the main issue here is the problem remains completely separate from the water bottle rocket scenario. The equations for the pipe bend case and the online calculator confirms that we should get these hundreds of pounds of force just for these pressure washers in common use when we bend around the hose. But that doesn’t seem to be the case when they are used. How could these be in common use if we would be getting 400 and 900 pound forces just by bending the hose around rearward!

Robert Clark

 

[Chestermiller]

I have no doubt you are quite knowledgeable in the topic. And actually I will want to ask another question that the link you gave discusses, this time in compressible flow. I’d like to get your feedback on that as well. I’ll get to that in a day or so.

But the main issue here is the problem remains completely separate from the water bottle rocket scenario. The equations for the pipe bend case and the online calculator confirms that we should get these hundreds of pounds of force just for these pressure washers in common use when we bend around the hose. But that doesn’t seem to be the case when they are used. How could these be in common use if we would be getting 400 and 900 pound forces just by bending the hose around rearward!

Robert Clark

Well, that 4200 psi seems way way way out of line. Here is a calculation that seems much more reasonable for the problem I posed in post #14.

From the Bernoulli equation, we have $$P_1+\rho\frac{v_1^2}{2}=P_2+\rho\frac{v_2^2}{2}$$ where the subscript 1 refers to an upstream location within the hose and the subscript 2 refers to the nozzle exit. In addition, the continuity equation tells us that $p_1A_1=p_2A_2$. At the nozzle exit, the pressure is atmospheric (zero gauge pressure), so we have
$$P_1=\rho\frac{v_2^2}{2}\left[1-\left(\frac{A_2}{A_1}\right)^2\right]$$For the case at hand, we have:
$$A_1=0.7126\ cm^2$$$$A_2=0.0792\ cm^2$$$$v_1=3.54\ m/s$$and$$v_2=31.86\ m/s$$So, from the above equation, we obtain $$P_1=5.01\ bars=72.7\ psi$$This, of course, is much less than 4200 psi, but certainly more realistic and reasonable.
To get the force that the nozzle exerts on the fluid (and, thus, the force that the fluid exerts on the nozzle) we must perform a macroscopic momentum balance: $$P_1A_1+F=\rho v_2A_2(v_2-v_1)$$ where F is the forward force that the nozzle exerts on the fluid and the right hand side of the equation represents the rate of change of momentum of the fluid passing through the nozzle. Combining these equations to solve for the force F gives:
$$F=-\rho\frac{v_2^2}{2}A_1\left(1-\frac{A_2}{A_1}\right)^2$$For the present case, we calculate $$F=-6.7\ lb$$This means that the hose and nozzle are exerting a force in the backward direction on the fluid (i.e., pulling back), and the fluid is exerting a force in the forward direction on the nozzle and hose. So the fluid is not exerting a backward force on the nozzle. The forward force of the fluid on the nozzle and hose causes the hose to become taught. The magnitude of the force F represents the tension in the hose.

Now, suppose that, in the case of the power shot, there is a reservoir of water down below that feeds fluid through a vertical section of 3/8" tubing to the horizontal section of tubing containing the nozzle. The vertical section is connected to the horizontal section by a 3/8" elbow. The next step will be to determine the horizontal force exerted by the water on the combination of horizontal and vertical section. This can be interpreted as the net horizontal reaction force on the system. Will that be OK with you?

 

[RobertGC]

Yes. Those numbers seem very reasonable. They are in accordance with the pressure values you commonly see such as those coming out of home faucets and water hoses, in the range of 60 to 80 psi, 4 to 5.3 bar.

But pressure washers are at far above these values, 2,000psi, 3,000psi, and even higher are the norm:

Home Depot Pressure Washers

The inner diameter of the hoses on such pressure washers are pretty much standardized at 1/4” for the lower end ones and 3/8” at the higher end.

I agree the water bottle rocket values for the force look reasonable. But when we look at the pipe bend force analysis. You get hundreds of pounds for the force on the bend which seems unreasonable considering such pressures washers in common use.

Robert Clark

 

[Chestermiller]

Yes. Those numbers seem very reasonable. They are in accordance with the pressure values you commonly see such as those coming out of home faucets and water hoses, in the range of 60 to 80 psi, 4 to 5.3 bar.

But pressure washers are at far above these values, 2,000psi, 3,000psi, and even higher are the norm:

Home Depot Pressure Washers

The inner diameter of the hoses on such pressure washers are pretty much standardized at 1/4” for the lower end ones and 3/8” at the higher end.

I agree the water bottle rocket values for the force look reasonable. But when we look at the pipe bend force analysis. You get hundreds of pounds for the force on the bend which seems unreasonable considering such pressures washers in common use.

Robert Clark

Well, then something isn't quite right, or we are missing something in the design. Maybe the 4 gpm is too low. We would have to get a look at the internal piping of the washer before being able to resolve this.

 

[256bits]

Well, then something isn't quite right, or we are missing something in the design. Maybe the 4 gpm is too low. We would have to get a look at the internal piping of the washer before being able to resolve this.

What is actually unreasonable?

 

[Chestermiller]

After examining some photos of power washer nozzles (with water jetting out) on the internet, a more clearcut picture is emerging. For a 0 degree nozzle (leading to maximum stagnation pressure), the jet diameter appears much smaller than I imagined. Your estimate of a 0.0455" diameter for the nozzle jet seems more realistic now. So in that case, we would have: $$A_1=0.7126\ cm^2$$$$A_2=0.0105\ cm^2$$$$v_1=3.54\ m/s$$and$$v_2=240\ m/s$$Based on this, the upstream pressure would be $$P_1=288\ bars=4180 psi $$ This would give a value of F = -448 lb for the. horzontal force of the nozzle on the fluid, and a force of +448 lb exerted by the flowing fluid on the nozzle (in the same direction as the fluid flow). This would also be the tension in the 3/8" tubing.

If there were a 90 degree vertical elbow in the 3/8" tubing upstream of the nozzle, say coming from a water reservoir, the horizontal force exerted by the elbow on the flowing fluid would be given by: $$-P_1A_1+F_x=\rho v_1^2A_1$$This gives a value of $$F_x=462\ lb$$ So the horizontal force that the fluid exerts on the elbow is 462 lb in the direction opposite to the flow. So the net horizontal force exerted by the flowing fluid on the combination of nozzle and elbow (and thus, on the internal tubing as a whole) is $$F_{net}=462-448=14\ lb$$This is also equal to just $$F_{net}=\rho v_2^2A_2=14\ lb$$This is the horizontal reaction force on the power washer. So, because of the presence of a nozzle and an elbow in the tubing, the tension in the tubing is about 450 lb, but, because of the change in direction afforded by the 90 degree elbow, the net horizontal reaction force on the power washer is only 14 lb.