annamal
- 393
- 33
Thread moved from the technical forums to the schoolwork forums
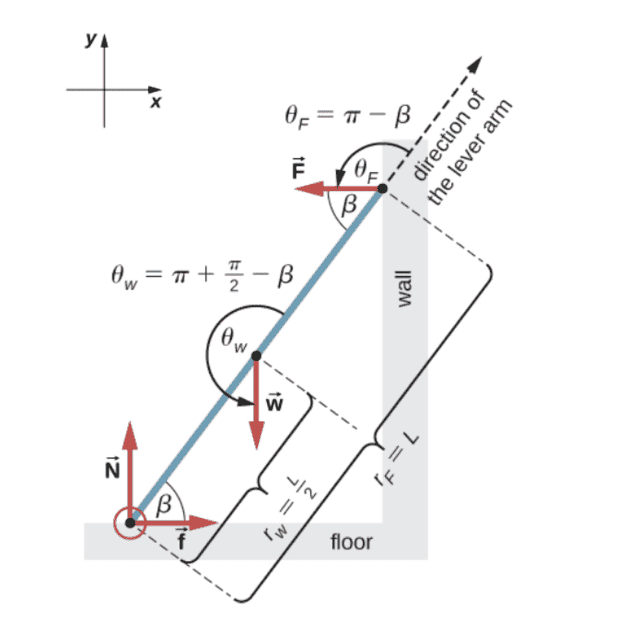
A ladder is leaning against a frictionless wall and the floor. The force F of the wall against the ladder is what is opposing static friction f at the floor. I don't understand how the force F causes the ladder to slide to the left on the floor unless opposed by friction force f. See picture below.
Last edited: