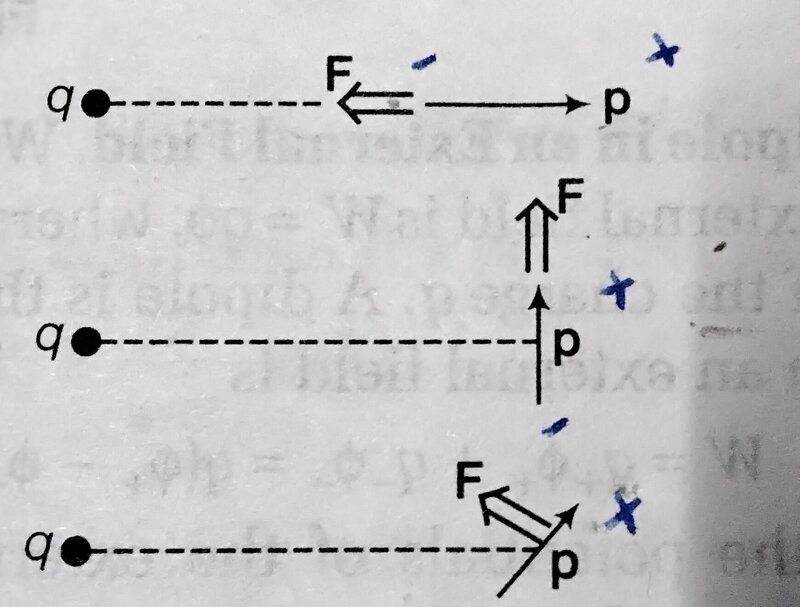
Something looks off (i.e., "wrong") with the problem statement. I'm hoping your instructor didn't give you a bad problem, but it's not unheard of. Then again maybe I'm missing something myself.
From what I can tell, middle and bottom parts look wrong, although maybe the middle part is a trick question.
You haven't shown any work so we're not allowed to help help you until you do. Allow me to correct your statement,
Shreya said:
Relevant Equations:: F=p*(partial derivative of E with respect to direction of p )
That's not quite right. The partial derivative is not necessarily in respect to the direction of \vec p, but rather with respect to the spatial coordinates. \vec F, \vec p, and \vec E are all vectors, and they should be all subject to the chosen coordinate system.
It's true that
\vec F = \left( \vec p \cdot \vec \nabla \right) \vec E
and in Cartesian coordinates this becomes,
\vec F = \left( p_x \frac{\partial}{\partial x} + p_y \frac{\partial}{\partial y} + p_z \frac{\partial}{\partial z} \right) \vec E
but that's still not enough to reconcile the middle and bottom parts, unless maybe I'm missing something.
- Is the dipole in question just an electric dipole (as opposed to a magnetic dipole), and nothing is presently moving?
- Are all three parts intended to be taken separately (i.e., not all charges are all present simultaneously)?
- Is there anything else in this problem that wasn't stated in the problem statement, such as other constraints or other charges or fields around?
- Can you use my equation in Cartesian coordinates (above) to show that there is something wrong with the middle and bottom figures?
[Edit: Nevermind. I was misinterpreting the problem statement. The diagrams are fine.]