Force to propel a sliding gate up a 2,4 degree incline?

[James Nilsen-Misra]

TL;DR

What force is needed to propel a sliding (rolling) gate up a 2.456° degree incline?
The Gate has a mass of 380 Kg.
The wheels have a diameter of 120 mm, Steel UGroove wheels, runing on a 12mm diameter round bar track. (To reduce rolling resistance larger wheels have been included.)

(Wondering what strain this would give a Centurion motor, D5 Evo, rated to be able to work a gate of Max 500kg but its pulling force needs to be 17kg start up and not exceeding 10Kg during running.

Figure A

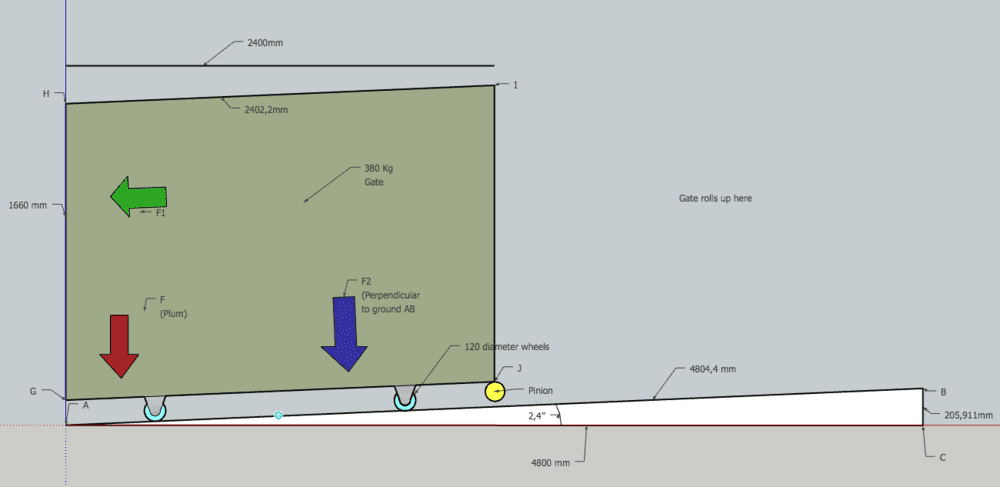
It slopes up from Left to Right (0.205911m Rise /4,8m run=4.28%)]

 

[Tom.G]

Total Force = <Operating-Force-If-Level> + (sin(2.5°) * <Weight-Of-Gate>)
= <Operating-Force-If-Level> + (0.0436 * 380kg)
= <Operating-Force-If-Level> + 16.56kG

Looks like you have exceeded the 10kg rating of the opener.

 

[James Nilsen-Misra]

Total Force = <Operating-Force-If-Level> + (sin(2.5°) * <Weight-Of-Gate>)
= <Operating-Force-If-Level> + (0.0436 * 380kg)
= <Operating-Force-If-Level> + 16.56kG

Looks like you have exceeded the 10kg rating of the opener.

Thanks so much Tom.G,

So then to work out the maximum mass the gate could be, would it be thus:

10kg/0.04285216=233.36046537kg?

Total Force = <Operating-Force-If-Level> + (sin(2.456°) * <Weight-Of-Gate>)
= <Operating-Force-If-Level> + (0.04285216 * 233.36046537kg )
= <Operating-Force-If-Level> + 9.99999999kg
<Operating-Force-If-Level> + 10kg

 

[James Nilsen-Misra]

Made this comparison of the various models and their power output.

 

[James Nilsen-Misra]

homework: https://www.dummies.com/education/s...he-force-needed-to-move-an-object-up-a-slope/

 

[Tom.G]

Not sure what is going on here.

Your first post stated the Centurion D10 was rated:

...not exceeding 10Kg during running.

The calculation in your post #3, correct as far as it goes, ignores the rolling resistance of <Operating-Force-If-Level>. This calculation could be valid if the rolling resistance is small enough to be ignored (unlikely).

Then the table in your post #4 shows the D10 is rated at 30kg force, not 10kg.

 

[James Nilsen-Misra]

Not sure what is going on here.

Your first post stated the Centurion D10 was rated:"...not exceeding 10Kg during running."

The calculation in your post #3, correct as far as it goes, ignores the rolling resistance of <Operating-Force-If-Level>. This calculation could be valid if the rolling resistance is small enough to be ignored (unlikely).

Then the table in your post #4 shows the D10 is rated at 30kg force, not 10kg.

Sorry for the confusion. Well spotted, the "...not exceeding 10Kg during running" came in an email from a supplier, but when comparing the specs of different models in the published manuals, I didn't find any reference to 10kgf.

Yeh, was thinking that the force to overcome resistance would be just a pinch more than the force to counter the mass of the gate+the additional weight due to the incline...

How much additional force to set it in motion, and how much force to keep it in motion do you think is reasonable?

I came across Steven Holzner's article on "Calculating the Force Needed to Move an Object Up a Slope" Physics I For Dummies, 2nd Edition. But I've just scanned it and need a bit more time to see and apply it.

Coming back to the table I'm keen on using the ET Nice Drive 600m, well priced and their service centre is close by, which they recommend every 18 months.

I want the gate design mass to comply with the motor's output, a 41kgf initial push to set in motion, and 30kgf to overcome resistance and keep moving! With a little extra for bad weather conditions.

Your help is greatly appreciated!

 

[anorlunda]

Just a little bit of gravel or small stones under those wheels could add greatly to the forces needed. Because of unforeseeable complications like that you need a safety factor of x2 or x3.