cheerspens
- 92
- 0
Homework Statement
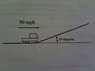
A runaway truck with a mass of 10,000 kg reaches an emergency pullout ramp moving at 90 mi/hr. As it plows through the deep sand spread over the pullout, it experiences a frictional force of 5000 Newtons opposing its motion. How high up the ramp will it rise?
Note that 1 mile=1609 meters.
Homework Equations
The Attempt at a Solution
So far I've only converted 90 mi/hr to 40.23 m/sec.
I'm totally confused on how to go about solving this problem. Maybe the fact that the ramp at 10 degrees is throwing me off?