Forces and Moments acting on an entire system.

[proctortom]

Homework Statement

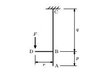
The ceiling-mounted bicycle rack (shown in "Capture" image in attachments) with dimensions p = 50 mm, q = 1000 mm and r = 150 mm for a bicycle that weighs F = 200 N.

The rack is to be made from two parts, ABC and BD, cut from a steel tube and then welded together at B.

Determine the forces and moments acting on the whole rack, ABCD.

Homework Equations

The only equations that I can see would be relevant here are the force and moment equations:
M = (F*d)
Ʃ M = 0
Ʃ F = o

The Attempt at a Solution

I have found M(of B) and M(of C) by doing the following:

M(of B) = 200*0.15 = 30Nm Clockwise

Therefore, 30 = 0.05*F(at A), so F(at A) = 600N

So... M(of C) = 1.05*600 = 630Nm Clockwise.

So I have found M at points B and C, and the force at A, however I am not confident that is what's required of the question. What does it mean by "the forces and moments acting on the whole rack ABCD"??

 

[haruspex]

There seems to be something missing in the problem statement. I gather from your attempted solution that there is a a horizontal force F_A at A.

I have found M(of B) and M(of C) by doing the following:

M(of B) = 200*0.15 = 30Nm Clockwise

Therefore, 30 = 0.05*F(at A), so F(at A) = 600N

If you are taking moments about B then you must consider a contribution from the force at C. It does not necessarily act vertically. Better might be to take moments about C.

 

[proctortom]

There seems to be something missing in the problem statement. I gather from your attempted solution that there is a a horizontal force F_A at A.

If you are taking moments about B then you must consider a contribution from the force at C. It does not necessarily act vertically. Better might be to take moments about C.

There is no acting force on A. I just calculated that because if there is a moment at B, then having the 200N force at D would be the equivalent of having a Force of 600N at A. Am I wrong?

 

[haruspex]

There is no acting force on A. I just calculated that because if there is a moment at B, then having the 200N force at D would be the equivalent of having a Force of 600N at A. Am I wrong?

Yes, that'd be wrong. If there's no force acting below B then the piece of the rack below B is irrelevant. Just take moments about C.
The question is fairly clear: what are all the forces and moments acting on the rack, assuming it stays in balance?

All that said, the question looks strange to me. It would be more reasonable if there were a horizontal force at A.

 

[Nickie]

I would like to clarify that the forces and moments acting on the whole rack ABCD refer to all the external forces and moments that are acting on the entire system, including the individual parts ABC and BD. This means that in addition to the forces and moments at points B and C, you also need to consider the forces and moments at points A and D, as well as any other external forces or moments that may be acting on the system.

To determine the forces and moments at points A and D, you can use the equations of equilibrium, Ʃ F = 0 and Ʃ M = 0, to find the unknown forces and moments. Additionally, you may also need to consider the geometry and dimensions of the system in order to accurately determine the forces and moments at points A and D.

It is important to note that the forces and moments acting on the whole system must be in equilibrium in order for the rack to remain stable. This means that the sum of all the forces and moments acting on the system must be equal to zero.

In conclusion, to fully determine the forces and moments acting on the whole rack ABCD, you need to consider all the external forces and moments acting on the system, including those at points A and D, and ensure that the system is in equilibrium.