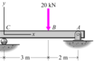
- #1
yellowbird321
- 19
- 2
Homework Statement
1.Explain how one with the help of the free body diagram can calculate forces and moments on the vertical cut line through the beam in a distance 1 m to the right from the point C.
2. Explain how one calculate size and distribution normal stress of the cut line. The beam is a I profile with moment of inerti I= 22,2*106 mm4 and height = 162 mm.
Homework Equations
Part 1.
∑Fx = 0 ∑Fy = 0 ∑Fz = 0
∑Mx = 0 ∑My = 0 ∑Mz = 0.Part 2.
The elastic flexure formula:
σx = - (Mr y / I)
The Attempt at a Solution
Part 1.
I have applied the equations of equilibrium to the full beam to determine the unknown forces acting on it.
+ ∑Ma = 0: -20 kN(2 m) + Cy(5.5 m) = 0 → 5.5Cy = 40 + 112.5 → Cy = 27,7 kN
↑ + ∑Fy = 0: -Ay – 20 kN + 27,7 kN = 0 → Ay = -20 + 27,7 → Ay = 7.7 kN
→ + ∑Fx = 0: Ax = 0 kN
This might be overdoing it however, since we are only asked about the forces and moments on the vertical cut line through the beam in a distance 1 m to the right from the point C.
Here I have attempted
+ ∑Ma = 0: -20 kN(2 m) + Cy(4 m) = 0 → 4Cy = 40 → Cy = 10 kN
↑ + ∑Fy = 0: -Ay – 20 kN + 10 kN = 0 → Ay = -20 + 10 → Ay = -10 kN
→ + ∑Fx = 0: Ax = 0 kN
Is this correct.
Part 2.
We are given:
I = 22,2*106 mm4
H = 162 mm.
So do we simply put the numbers in
σx = - (Mr y / I)
= - 27,7 kN x 0,162 m / 22,2*106 mm4 .
This part confuses me. Help would be appriciated.