Forces applied to a block on a ramp

[yesmale4]

Homework Statement

A block is resting on a ramp as shown in the figure below. You can change the inclination angle θ by raising one end of the ramp. The block has a mass m = 7.5 kg. At the interface between the ramp and the block, the coefficient of static friction is μs = 0.40, and the coefficient of kinetic friction is μk = 0.320.
the question:
Now let's go back and consider the static situation again. Let the angle θ be the angle you calculated in the first part of this problem, θ. Assume that a horizontal (parallel to the surface of Earth) force directed to the right is applied to the block. This horizontal force [(F)\vec] has a magnitude of 40 Newtons. Calculate the force due to static friction, [(f)\vec]s for this new situation, assuming that the block does not slip. Define your coordinate system such that your answer is positive if [(f)\vec]s is directed up the plane, and negative if [(f)\vec]s is directed down the plane.

Relevant Equations

f=ma

hey I am really hope for some help becuase i don't know what I am doing wrong, the angle of the first part is 21.801.
here is my solution i would like to know what I am doing wrong

 

[kuruman]

You show force F directed up the incline. The problem says it is horizontal, parallel to the surface of the Earth. That should change your solution, no?

 

[yesmale4]

You show force F directed up the incline. The problem says it is horizontal, parallel to the surface of the Earth. That should change your solution, no?

i understand but i don't know how to draw the force In this direction

 

[Lnewqban]

i understand but i don't know how to draw the force In this direction

 

[kuruman]

 

[nasu]

To OP: Your problem statement is incomplete. It refers to an angle found in the first part but there is no first part.

 

[kuruman]

To OP: Your problem statement is incomplete. It refers to an angle found in the first part but there is no first part.

The first part is not needed to answer the question in the second part. OP quotes the angle in post #1:

hey I am really hope for some help becuase i don't know what I am doing wrong, the angle of the first part is 21.801.
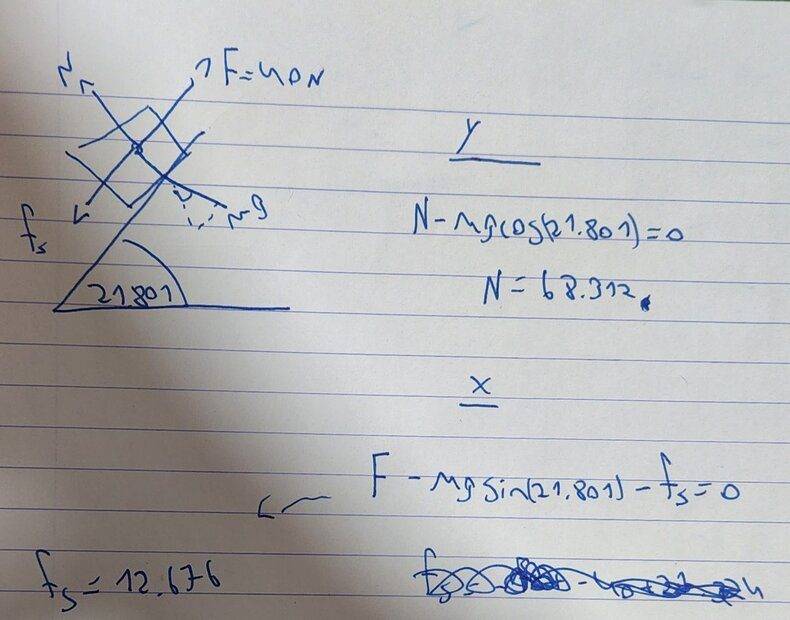
here is my solution i would like to know what I am doing wrong

 

[yesmale4]

View attachment 298727

i don't know why but it still wrong i disassembled F into components:
x - Fcos(21.801)
y- Fsin(21.801) - doesn't matter actually
and than i did
Fcos(21.801)-mgsin(21.801)-Fs=0
Fs=9.814N
and its wrong i would like to know what i did wrong

 

[kuruman]

Your method is correct and agrees with my calculation. Is this the kind of problem that is scored by a machine on a website? If so, I see three four possibilities in order of likelihood: (a) you did not read the problem carefully enough (it happens to the best of us); (b) the angle of the incline is not 21.8°; (c) if 21.8° has already been marked as "correct" but is actually borderline within the tolerance of the scoring algorithm, then you might have roundoff errors that pushed the solution to the second part outside the algorithm's tolerance; (d) the algorithm uses the wrong formula to do its job; .

My recommendation is to redo the first part and make sure you avoid all roundoffs. If the angle is still 21.801°, show your solution to your instructor and ask for an explanation.

Edited to incorporate @haruspex's observation in post #12.

 

[Lnewqban]

i don't know why but it still wrong i disassembled F into components:
x - Fcos(21.801)
y- Fsin(21.801) - doesn't matter actually
and than i did
Fcos(21.801)-mgsin(21.801)-Fs=0
Fs=9.814N
and its wrong i would like to know what i did wrong

That is not correct, as the new force F increases the value of the normal force; therefore, Fs increases.
Prior to application of F, the magnitude of Fs was mgcosθ or 27.32 N.
As N1>N, Fs1>Fs

That is the reason you apply greater force onto the brake pedal of a car or truck to reduce the braking distance, to increase the value of friction force (Fk in that case) via increasing the value of the force that is perpendicular to the brake disc or drum.

 

[kuruman]

That is not correct, as the new force F increases the value of the normal force; therefore, Fs increases.

F_s is what is necessary to provide the observed acceleration in the direction parallel to the incline. OP's equation balancing the forces in that direction does exactly that. Increasing the normal force increases the maximum value of the static friction but not the static friction that is needed to prevent the block from sliding.

 

[haruspex]

Fs=9.814N
and its wrong i would like to know what i did wrong

"Define your coordinate system such that your answer is positive if $\vec f_s$ is directed up the plane, and negative if $\vec f_s$ is directed down the plane."

 

[kuruman]

"Define your coordinate system such that your answer is positive if $\vec f_s$ is directed up the plane, and negative if $\vec f_s$ is directed down the plane."

Aaah! I missed that.

 

[nasu]

The first part is not needed to answer the question in the second part. OP quotes the angle in post #1:

Yes, but it is needed for other people to understand the question. What is the meaning of that angle?

 

[kuruman]

Yes, but it is needed for other people to understand the question. What is the meaning of that angle?

It can be identified as the angle of repose, $\tan(\theta_r)=\mu_s$ because $\tan(21.801^o)=0.4$. The missing part (a) probably asks something like "The coefficient of static friction between block and incline is $\mu_s=0.4$ and the block is on the verge of sliding. Find the angle of the incline."

In part (a), the force of static friction is up the incline, it has magnitude 27.3 N and the block is just about ready to slide. The OP has found that In part (b) the force of static friction changes direction to down the incline and has magnitude 9.81 N.

It might be interesting to find an upper limit for the external force F beyond which the block will start sliding up the incline. I will not divulge that number lest it is part (c) of this problem and OP has not told us yet. All I can say is that it is greater than 40 N so the assertion in the statement of the problem that the block does not slide when F = 40 N is justified.

 

[yesmale4]

"Define your coordinate system such that your answer is positive if $\vec f_s$ is directed up the plane, and negative if $\vec f_s$ is directed down the plane."

So because i put Fs down the plane the correct answer should be -9.814N ?

 

[haruspex]

So because i put Fs down the plane the correct answer should be -9.814N ?

Yes.

 

[nasu]

It can be identified as the angle of repose, $\tan(\theta_r)=\mu_s$ because $\tan(21.801^o)=0.4$. The missing part (a) probably asks something like "The coefficient of static friction between block and incline is $\mu_s=0.4$ and the block is on the verge of sliding. Find the angle of the incline."

In part (a), the force of static friction is up the incline, it has magnitude 27.3 N and the block is just about ready to slide. The OP has found that In part (b) the force of static friction changes direction to down the incline and has magnitude 9.81 N.

It might be interesting to find an upper limit for the external force F beyond which the block will start sliding up the incline. I will not divulge that number lest it is part (c) of this problem and OP has not told us yet. All I can say is that it is greater than 40 N so the assertion in the statement of the problem that the block does not slide when F = 40 N is justified.

You did not get this from the OP. My point was that the OP should explain all this and not you or some other forum participant.