Forces on particle in complex motion relative to ground observer

[vcsharp2003]

Homework Statement

What would be the forces acting on the particle in groove for problem given below when the observer is a ground observer i.e. in an inertial frame of reference? So, observer is not in rotating cabin which would be a non-inertial reference frame of reference.

I know that at any instant of time, the particle will have a tangential and a radial centripetal acceleration but cannot figure out the free body diagram of the particle. As a result of tangential + radial acceleration, the particle will traverse a complex curved path relative to ground observer.

Relevant Equations

F=m(ww)r ( m times w squared times r where w is angular velocity of rotating object)

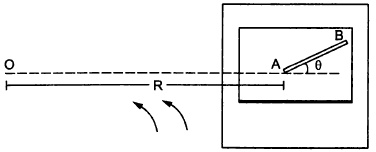
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular path of radius R. A smooth horizontal groove AB of length L(<<R) is made on the surface of the table. The groove makes an angle θ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by the particle to reach the point B.

 

[PeroK]

What happens to the particle if $\theta = 0$?

What happens if $\theta = \frac{\pi}{2}$?

Note that the time taken for the particle to move from A to B is the same, whatever reference frame you use to analyse the problem. Have you learned about fictitious or inertial forces?

 

[vcsharp2003]

What happens to the particle if $\theta = 0$?

What happens if $\theta = \frac{\pi}{2}$?

Note that the time taken for the particle to move from A to B is the same, whatever reference frame you use to analyse the problem. Have you learned about fictitious or inertial forces?

Yes I know that the fictitious force called centrifugal force is to be used when observer is in the same rotating frame of reference. But I wanted to know if we can solve this problem without using the rotating frame of reference i.e. using ground as frame of reference and applying the fact that the net force's component along radius provides a radial acceleration of ω²r.

When θ = 0 then I still have the same doubt when drawing free body diagram of the particle. There will be no friction force on particle since groove is smooth, so only its weight and the the normal reaction force acts on the particle which has no component along the radius due to it being perpendicular to radius. If my previous statement is true then what "real" force contributes to the centripetal force in the case when θ = 0? I would guess mg = R where R is normal reaction in this case. (Frame of reference is ground)

When θ = 90^o then its easy to understand the free body diagram since mg = R where is R is normal reaction but then again I have the same question that which force would contribute to centripetal acceleration in this case.(Frame of reference is ground)

 

[PeroK]

Yes I know that the fictitious force called centrifugal force is to be used when observer is in the same rotating frame of reference. But I wanted to know if we can solve this problem without using the rotating frame of reference i.e. using ground as frame of reference and applying the fact that the net force's component along radius provides a radial acceleration of ω²r.

In the ground frame, there are three forces on the particle: gravity, the lateral constraining force of the groove, and the normal force of the groove.

When θ = 0 then I still have the same doubt when drawing free body diagram of the particle. There will be no friction force on particle since groove is smooth, so only its weight and the the normal reaction force acts on the particle which has no component along the radius due to it being perpendicular to radius. If my previous statement is true then what "real" force contributes to the centripetal force in the case when θ = 0? I would guess mg = R where R is normal reaction in this case. (Frame of reference is ground)

In this case, there is no centripetal force on the particle.

When θ = 90^o then its easy to understand the free body diagram since mg = R where is R is normal reaction but then again I have the same question that which force would contribute to centripetal acceleration in this case.(Frame of reference is ground)

In this case, the centripetal force is provided by the vertical constraining wall of the groove.

 

[vcsharp2003]

In the ground frame, there are three forces on the particle: gravity, the lateral constraining force of the groove, and the normal force of the groove. In this case, there is no centripetal force on the particle.In this case, the centripetal force is provided by the vertical constraining wall of the groove.

Thanks for the excellent answer. It makes it much more clear for me but I need to think over your answers to properly understand. The groove is always horizontal on the table since the surface of table is always horizontal. (θ is not meaning that the grove is inclined above the horizontal but its just the angle made by the groove with the radius)

So, in the case of θ = 0 how would the particle move along the groove? I am guessing that still some component of reaction from groove on particle along the radius would contribute to centripetal acceleration along OA since particle is rotating with table at any instant of time.

In the case of θ =90^o, how would the particle move along the groove?

 

[PeroK]

The groove is always horizontal on the table since the surface of table is always horizontal. (θ is not meaning that the grove is inclined above the horizontal but its just the angle made by the groove with the radius)

Okay, I misread the diagram. I assumed $\theta$ was an angle with the vertical. Apologies.

As you say, it should be simple to analyse this in the rotating frame with the fictitious centrifugal force.

To analyse it in the ground frame, you will need the equation for acceleration in polar coordinates. In which case it may be better to rename $\theta$ to $\beta$ to avoid confusion with the conventional polar angle $\theta$.

 

[vcsharp2003]

Okay, I misread the diagram. I assumed $\theta$ was an angle with the vertical. Apologies.

As you say, it should be simple to analyse this in the rotating frame with the fictitious centrifugal force.

To analyse it in the ground frame, you will need the equation for acceleration in polar coordinates. In which case it may be better to rename $\theta$ to $\beta$ to avoid confusion with the conventional polar angle $\theta$.

If we consider the case shown in diagram, then what real forces are acting on the particle? I think they are

• weight mg acting vertically downwards
• some force from the groove on the particle and I am guessing that this force would resolve into a normal reaction R₁ and a force R₂ directed in radial direction towards O
• from above forces we would have R₁= mg and R₂ = mrω²
• probably there would another component of force from groove on particle directed along the tangential direction R₃. So force from groove on particle would have components along x, y and z axes.

 

[PeroK]

If we consider the case shown in diagram, then what real forces are acting on the particle? I think they are

• weight mg acting vertically downwards
• some force from the groove on the particle and I am guessing that this force would resolve into a normal reaction R₁ and a force R₂ directed in radial direction towards O
• from above forces we would have R₁= mg and R₂ = mrω²
• probably there would another component of force from groove on particle directed along the tangential direction R₃. So force from groove on particle would have components along x, y and z axes.

Not quite. Gravity is irrelevant. As the groove is smooth, the force on the particle is always normal to the surface of the groove. Let's look at a simple radial groove, where $\beta = 0$. I.e. the force is always instantaneously in the tangential direction: $\hat \theta$.

But, this is the critical point, if you look at the equation for acceleration in polar coordinates things are not as simple as in Cartesian coordinates. This is,ultimately, because the polar unit vectors $\hat r, \hat \theta$ change with position. If you have a force $\vec F = F \hat \theta$, then using $\vec F = m \vec a = m \ddot{\vec r}$ we have:
$$(\ddot r - r\dot \theta^2)\hat r + (r\ddot \theta + 2\dot r \dot \theta)\hat \theta = \frac{F}{m}\hat \theta$$
And we can see that $\dot r \ne 0$.

There is, I think, a critical point here about the importance of mathematics. If you don't use the mathematics, then you could argue all your life about this. The solution lies in understanding the mathematics of polar coordinates.

 

[PeroK]

PS just to avoid any confusion. The above analysis assumed a force of constant magnitude, whereas in the simple groove scenario, the constraint is $\ddot \theta = 0$ and we can see that $F$ varies with time in that scenario - but is always in the tangential direction.

PPS It's worth analysing both these scenarios in polar coordinates!

 

[vcsharp2003]

PS just to avoid any confusion. The above analysis assumed a force of constant magnitude, whereas in the simple groove scenario, the constraint is $\ddot \theta = 0$ and we can see that $F$ varies with time in that scenario - but is always in the tangential direction.

PPS It's worth analysing both these scenarios in polar coordinates!

A solution to this problem that I saw from someone else is as below. The person assumed no forces were acting on the particle other than centrifugal force (mg would cancel with R). But it makes little sense to me. His answer is matching with the answer given for this problem.

 

[PeroK]

A solution to this problem that I saw from someone else is as below. The person assumed no forces were acting on the particle other than centrifugal force (mg would cancel with R). But it makes little sense to me. His answer is matching with the answer given for this problem.

View attachment 280648

That's the easy way - using the rotating reference frame. I thought you wanted to do it the hard way using the ground frame?

That solution is simply what happens to the particle if you give it a constant force in the direction of the arrow. The force is canceled out in the direction normal to the groove and moves smoothly along the groove.

Note that it's the same problem as an object sliding down a ramp inclined at $\theta$ to the vertical, with a gravitational force $g = mR \omega^2$.

 

[vcsharp2003]

That's the easy way - using the rotating reference frame. I thought you wanted to do it the hard way using the ground frame?

That solution is simply what happens to the particle if you give it a constant force in the direction of the arrow. The force is canceled out in the direction normal to the groove and moves smoothly along the groove.

Note that it's the same problem as an object sliding down a ramp inclined at $\theta$ to the vertical, with a gravitational force $g = mR \omega^2$.

I see a paradox in the simple solution. It's implying that besides the normal reaction and weight of particle mg there are no external forces. If we assume this as true then for an observer on Earth there are no forces on the particle that can supply the centripetal acceleration. Do you get the paradox arising due to the simple solution?

 

[PeroK]

I see a paradox in the simple solution. It's implying that besides the normal reaction and weight of particle mg there are no external forces. If we assume this as true then for an observer on Earth there are no forces on the particle that can supply the centripetal acceleration. Do you get the paradox arising due to the simple solution?

I explained that in post #8. The "paradox" is due to a tangential force producing radial motion.

To see this imagine a particle at rest at coordinates $(1,0)$ (i.e. on the x-axis). Give the particle a brief impulse in the positive y-direction. The particle moves along the straight line $(1, y)$.

But, by your logic, the initial impulse was "tangential" to the circle centred at the origin, so the motion should remain "tangential": i.e. the particle should move in a circle!

It doesn't because as it moves in a straight line the local polar basis vectors change and the straight line motion is no longer in the $\hat \theta$ direction but has a $\hat r$ component as well. And it's clear that the tangential impulse produced tangential and radial motion.

 

[vcsharp2003]

I explained that in post #8. The "paradox" is due to a tangential force producing radial motion.

To see this imagine a particle at rest at coordinates $(1,0)$ (i.e. on the x-axis). Give the particle a brief impulse in the positive y-direction. The particle moves along the straight line $(1, y)$.

So, relative to an observer on the rotating table the particle appears to move either in +ve y or -ve y direction?

When we use an accelerated frame of reference, then we need to include -ma force on the particle where +a is acceleration of accelerated frame. In addition, we must include all other real forces on the particle. Is that right? In simple solution it's mentioned only -ma force i.e. mrw² as the force on the particle. Should not the other real forces be considered when observing from the rotating table?

 

[PeroK]

So, relative to an observer on the rotating table the particle appears to move either in +ve y or -ve y direction?

When we use an accelerated frame of reference, then we need to include -ma force of the particle where +a is acceleration of accelerated frame. In addition, we must include all other real forces. Is that right? In simple solution it's mentioned only -ma force i.e. mrw². Should not the forces be considered?

Technically, you have the Coriolis force as well. But, that acts perpendicular to the velocity of the particle: in this case that is the fictitious force that balances out the normal force from the groove in the rotating frame. That leaves only the appropriate component of the centrifugal force acting along the groove.

It's a good point.

 

[vcsharp2003]

The force is canceled out in the direction normal to the groove and moves smoothly along the groove.

What force cancels the force perpendicular to the groove of centrifugal force? Is the the normal reaction on the particle from groove in the plane of table?

I think the FBD of forces within the plane of table are as below. R₁ is normal reaction on particle from groove and mrω² is centrifugal force on the same particle since observer is on rotating table.

 

[PeroK]

What force cancels the force perpendicular to the groove of centrifugal force? Is the the normal reaction on the particle from groove in the plane of table?

In the rotating reference frame it's the Coriolis force.

 

[vcsharp2003]

In the rotating reference frame it's the Coriolis force

Isn't coriolis force same as centrifugal force?

 

[PeroK]

Isn't coriolis force same as centrifugal force?

Not at all. Just search online.

 

[vcsharp2003]

Not at all. Just search online.

I looked up Coriolis force in a rotating frame of reference and found that when observer is in a rotating frame of reference then another fictitious force comes into the picture called Coriolis force having a magnitude and direction given by the following cross product: $-2m ~ \vec {\omega} \times \vec v$, where $\vec {\omega}$ is the angular velocity vector that will perpendicular to the plane of rotating frame and $\vec v$ is the velocity of mass m being observed relative to rotating frame of reference.

Coriolis force is not centrifugal force and the only similarity between them is that they are both fictitious forces and come into the picture only when observer is in a rotating frame of reference.

Does this sound correct?

 

[PeroK]

I looked up Coriolis force in a rotating frame of reference and found that when observer is in a rotating frame of reference then another fictitious force comes into the picture called Coriolis force having a magnitude and direction given by the following cross product: $-2m ~ \vec {\omega} \times \vec v$, where $\vec {\omega}$ is the angular velocity vector that will perpendicular to the plane of rotating frame and $\vec v$ is the velocity of mass m being observed relative to rotating frame of reference.

Coriolis force is not centrifugal force and the only similarity between them is that they are both fictitious forces and come into the picture only when observer is in a rotating frame of reference.

Does this sound correct?

Yes. If you go back to post #8, I gave you the formula for acceleration in polar coordinates:
$$(\ddot r - r\dot \theta^2)\hat r + (r\ddot \theta + 2\dot r \dot \theta)\hat \theta = \ddot{\vec r} = \frac{\vec F}{m}$$ And you can see that there is a "centrifugal" term in the $\hat r$ direction and a Coriolis term in the $\hat \theta$ direction. If you change to the rotating reference frame, then these terms become the fictitious forces.