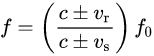xxxyyy
- 14
- 2
- TL;DR
- Contradictory results in Doppler effetc formulas
Hi,
I know the usual formula for both moving source and receiver in a static medium (from wiki):
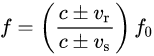
Is ir correct?
What about when the medium is moving too?
I can't seem to find an answer, and worst, I'm finding contradicting ones.
For example, when the source and the receiver are moving at the same speed in the same direction, someone says there should be no Doppler shift in frequency, and so does the prevoius formula.
But then, picture this: source and receiver both stationary in moving medium (wind blowing from the source to the receiver, to fix the ideas), then the receiver hears a higher frequency because wavefronts are pushed towards it, and the formula to be used is that of a fixed source and moving receiver, moving towards the source at the speed of the wind in a stationary medium.
The two experiments are physically the same... but the formulas give differtent results.
So, which formula is right?
What's going on here?
Thank you!
I know the usual formula for both moving source and receiver in a static medium (from wiki):
Is ir correct?
What about when the medium is moving too?
I can't seem to find an answer, and worst, I'm finding contradicting ones.
For example, when the source and the receiver are moving at the same speed in the same direction, someone says there should be no Doppler shift in frequency, and so does the prevoius formula.
But then, picture this: source and receiver both stationary in moving medium (wind blowing from the source to the receiver, to fix the ideas), then the receiver hears a higher frequency because wavefronts are pushed towards it, and the formula to be used is that of a fixed source and moving receiver, moving towards the source at the speed of the wind in a stationary medium.
The two experiments are physically the same... but the formulas give differtent results.
So, which formula is right?
What's going on here?
Thank you!
Attachments
Last edited by a moderator: