Goldhelmeth
- 1
- 0
- Homework Statement
- Calculate the ionization potential reduction of He1+ in the framework of the Bohr model and
interpret the results concerning the existence of ground and excited states:
a) in the center of the sun,
b) for the average density of the sun at kTe=1300 eV.
- Relevant Equations
- *see images
Hello,
Firstly I am not sure of understanding the problem, I believe that this reduction is related to a high density plasma where the free electrons are very close to the ions and so the ions cannot be considered as separate bodies... I also believe it affects the ground energy state of electrons inside hydrogen like atoms (helium +1).
For solving this problem I found that every solutions used the Stewart and Pyatt model. This model uses the debeye lengh. But as you can see it uses an other model... I wished I could provide more to the community to start with but I have been on this problem for hours and I cannot find annything...
Thank you for any help you may provide !
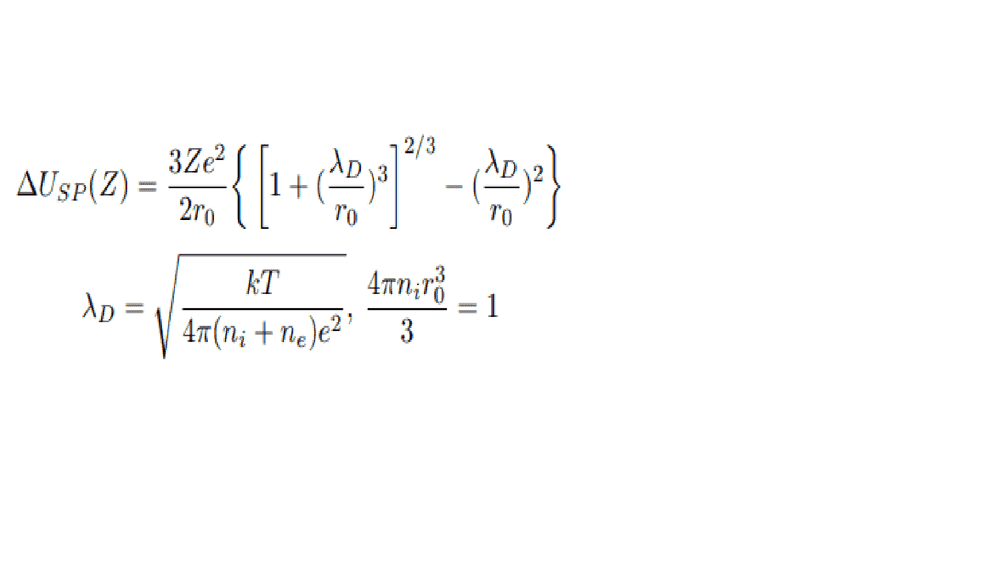
Firstly I am not sure of understanding the problem, I believe that this reduction is related to a high density plasma where the free electrons are very close to the ions and so the ions cannot be considered as separate bodies... I also believe it affects the ground energy state of electrons inside hydrogen like atoms (helium +1).
For solving this problem I found that every solutions used the Stewart and Pyatt model. This model uses the debeye lengh. But as you can see it uses an other model... I wished I could provide more to the community to start with but I have been on this problem for hours and I cannot find annything...
Thank you for any help you may provide !