Four-Bar Parallel Linkage Pendulum

[grvlfun]

Hello, I'm new here and I'm looking for advice regarding some calculations of a device I constructed/should construct.

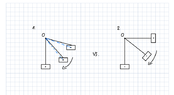
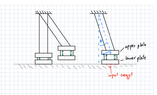
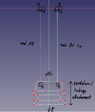
It's a 4 bar (parallel) linkage system, which is used like a pendulum. It is released from a certain height, with just the gravity acting on it.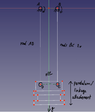

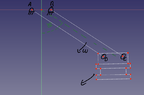
I understand how to calculate the potential energy and kinetic rotational energy for a simple pendulum consisting of a rod with an attached mass, using the moment of inertia. However, with this linkage system, I don't know how to include the moment of inertia for the rod AD and the rod BC, as they are turning around a separate axis. To make it even more difficult, the rods are crossing each other once it reaches a certain angle/height, twisting the attachement.
(While in theory I think this shouldn't be the case for a perfect parallel system, here there's a minimal, but I think negligible length difference between the rods AD and BC).

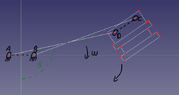How should I proceed to calculate the angular velocity at the center of gravity of the device?

My approach:
1. calculate the center of mass in a certain position.
2. calculate the potential energy in this position.
3. calculate the angular velocity based on the potential energy and kinetic rotational energy. However, at this step I don't know on how to include the moment of inertia of the 2 rods, which have 2 different axes.

For steps 1 and 2: I think once the twisting of the attachement is reached, the center of gravity is changing constantly, making it necessary to maybe solve the equations for the angular velocity step by step?

 

[Baluncore]

Welcome to PF.

(While in theory I think this shouldn't be the case for a perfect parallel system, here there's a minimal, but I think negligible length difference between the rods AD and BC).

The length variation of the parallel links should be less than the clearance of the pin bearings. If such a change is not implemented in the model, the angular acceleration of the load could become extreme as it passes through the 90° point. Something must/will give to eliminate those huge forces associated with rotation of the load in the model. The links could stretch, the pins could bend, or the bearings could have some slack.

 

[grvlfun]

First: The rods are made of metal with holes drilled in them, and threaded bars are used as axes. There are no bearings yet and there is definitely some play in every direction, as the construction itself is just a prototype and not very precise, but it's working. To simulate the movement in my sketch (here: Freecad), I had to make one rod minimally shorter than the other one, in order to replicate the crossing of the rods.

Second: The attachment consists of an upper and lower plate, with the lower plate being able to move up and down. Once the pendulum is released, the lower plate will hit the ground and will be pulled over the ground by the upper plate. A full 360° turn isn't intended.

Therefore, for now the goal would be to calculate the angular velocity based on a certain starting position with regard to the moments of inertia of the different components.
I'd be also happy for every advice regarding literature or other sources which could be useful in calculating this.

 

[Baluncore]

Therefore, for now the goal would be to calculate the angular velocity based on a certain starting position with regard to the moments of inertia of the different components.

You do not need to calculate the angular rotation. For a parallel bar linkage the pendulum will needs to remain very close to horizontal. I will try to explain why, without resorting to books about chaos.

If the bars are almost the same length then the rotation needed to pass the ±90° point will be catastrophic. There will be a chaotic branching point on approaching ±90° where a decision will need to be made as to which way to rotate bob. The closer the bars are to equal length the closer the angular acceleration will be to infinite, with the sign being chaotically unpredictable.

The problem you see in the length of the pendulum also exists in the horizontal bar length measurements. For a parallel bar linkage, it is the sum of a combination of link lengths that must be equal;
a+b = c+d ; (at –90°) on one side, must be true, while on the other side;
a+d = b+c ; (at +90°) must be true.
If the lengths are fixed then there can be nowhere to hide the thermal expansion errors.

The problem can only be resolved by making sure that the bar lengths plus the bearing clearances can adjust themselves to be identical. If there is no available clearance, then one of the support pins would need to be free to move horizontally by about 1 mm. That also resolves the chaotic branch in direction of rotation problem that you would need to model at ±90°.

 

[grvlfun]

Okay, hopefully I've got your point correctly: by angular rotation you mean the angular rotation around every joint, by every rod/bar? And once it starts twisting, the calculation can become impossible/difficult as it is not sure in which direction the twisting happens once it is released?

However in the constructed device, the rotation of the bob is always happening in the same direction and it works 'flawless', maybe because it is free to move horizontally by about 1 mm or because it has play at the holes for the axis.

Is there any way then, I could do a raw estimation/calculation of the expected speeds of the centre of the attachment when it is released from a certain height? E.g. break it down to resemble a simple pendulum and then calculate the potential energy and kinetic energy from there on?

 

[Baluncore]

Is there any way then, I could do a raw estimation/calculation of the expected speeds of the centre of the attachment when it is released from a certain height?

Yes. Conservation of energy tells you that the potential energy at the height it is dropped from will be converted to kinetic energy at the lowest point. Assume the bob remains horizontal.
½·m·v² = m·g·h
If the suspension rods are light weight, you might initially ignore them. Then you do not need to know the centre of mass of the bob, only the change in height.

 

[grvlfun]

The suspension aren't light weight, they account for over 50% of the total weight. And that's were I struggle in how to incorporate them into the calculation.
For a pendulum turning around 1 axis, you take the moment of inertia of the rod and the bob to calculate the velocity at the centre of the gravity the whole system. But how do you do it in this case with 2 rods turning around 2 separate axes?
Here are 2 sketches on what I mean.
Simple pendulum 1 axis

4 bar pendulum 2 axes


Is it possible to use an imaginary turning point O on whose axis the centre of gravity lies, in order to simplify the calculation?

 

[Baluncore]

But how do you do it in this case with 2 rods turning around 2 separate axes?

Since the rods are now moving in parallel, you can simplify the analysis by modelling one rod having twice the mass, halfway between the original two rods.

Since the bob does not rotate, you treat the bob as a separate body.

 

[grvlfun]

Okay thank you already a lot.

Concerning the bob, how should I treat this one as a separate body? As it remains parallel and therefore not changing its orientation, does this influence the moment of inertia, respectively the calculation?


Here you have 2 cases.
- Case 1: the bob remains parallel to the ground.
- Case 2: the bob changes its orientation.
In case 1, the center of mass of the bob changes it orientation compared to the center of mass of the rod? While in case 2, both remain on the same line.

 

[erobz]

Okay thank you already a lot.

Concerning the bob, how should I treat this one as a separate body? As it remains parallel and therefore not changing its orientation, does this influence the moment of inertia, respectively the calculation?
View attachment 300755

Here you have 2 cases.
- Case 1: the bob remains parallel to the ground.
- Case 2: the bob changes its orientation.
In case 1, the center of mass of the bob changes it orientation compared to the center of mass of the rod? While in case 2, both remain on the same line.

I think in case (2) you treat the MOI (for the hung mass) as:

$$ I_O = I_G + m r^2 $$

and in case (1)

$$ I_O = m r^2 $$

 

[Baluncore]

Concerning the bob, how should I treat this one as a separate body? As it remains parallel and therefore not changing its orientation, does this influence the moment of inertia, respectively the calculation?

Given the angle of the rod, you must distribute the converted potential energy to the bob and the rod in a 3 way split.
I would solve numerically for the angular velocity of the rod in that position.
The kinetic energy will then be in the bob centre of mass, the rod centre of mass, and the angular velocity of the rod.

 

[grvlfun]

I don't quite understand how you intend to distribute the converted potential energy in a 3 way split?

in steps:
1. take the 2 rods (3 in this case, as one side consists of 2 rods, while the other side only has 1 rod, so double the weight) and treat it as a uniform rod. Where should this 'new' rod be attached to bob?
2. calculate the centre of gravity of the rod and bob?
3. calculate the potential energy based on the centre of gravity?
4. distribute the potential energy between the bob and rod? How?
5. calculate the angular velocity based on the inertial moment of the bob and the rod by their respective potential energy?

Please correct on what steps are wrong and would you also please elaborate in how to perform this 3 way split?

 

[Baluncore]

Please correct on what steps are wrong and would you also please elaborate in how to perform this 3 way split?

0. We assume for the computation that the bob does NOT rotate.
1. The three rods remain in the structure, but are treated as one virtual rod during computation.
2. The centre of gravity of the combined rods and bob is not required. Since the bob does not rotate, only the velocity and height of the bob is important. Assume it is a lump at the end of the combined rods.
3. Specify the angle of the rods. The height of the bob, and the virtual rods CofG position is then known.
4. Use an iterative, or similar to Newton's method to solve for angular velocity, start with a guess, or use the previous value of the angular velocity. Repeat step 5 to search for error zero.
5. The solution will be the angular velocity when energy is balanced = conserved.
PE( initial ) = PE( rods ) + PE( bob ) + KE_linear( bob ) + KE_angular( rods ) + error.
6. You will have computed the wanted linear velocity of the bob.

 

[grvlfun]

Thank you.
For steps 4 and 5:
Is the Newton's Method necessary? As with KE_linear = 0.5*m*v², with v = r*ω -> KE_linear = 0.5*m*(r*ω)² and then you would get an equation:
PE(initial) = PE(rods) + PE(bob) + KE_linear(bob) + KE_rotational(rods)
without the error where one just must solve for ω²?

Please take a look at this sketch to see if I got your ideas right.


A further question/thought: KE_linear here becomes 0.5*m*r²*ω² with m*r² then being the Moment of Inertia. This is also what

I think in case (2) you treat the MOI (for the hung mass) as:

$$ I_O = I_G + m r^2 $$

and in case (1)

$$ I_O = m r^2 $$

actually mentioned for case (1). Why? Why is the MoI here just m*r² and the distance to the axis is not taken into account?

 

[erobz]

The total MoI isn't $mr^2$, that was just the MOI of the Bob ( when its not rotating with the assembly ).

The Total MoI of the system about $O$ :

Let:
$m_r$ be the mass of the "virtual rod"
$r$ is the length of that rod
$I_r$ is the MoI of the rod about an axis parallel to the axis of rotatiation passing through its CoM
$m$ is the mass of the bob


Then using the Parallel Axis Theorem:

$$ I_O = I_r + m_r \left( \frac{r}{2} \right)^2 + m r^2 $$

Does that answer your question about the MoI better?

The thing is I'm not sure if this is what Baluncore is suggesting in the model they have in mind using energy considerations. This is the MoI I would use beginning with Newtons Second Law. When using energy, maybe you have to be careful about energy accounting?

Also, I could be wrong, and just confusing you more...

 

[grvlfun]

I didn't mean the total MoI, but just the one of the bob.
For the rod, as you described, the distance of an axis parallel to the axis of rotation is taken into account.
Why isn't this the case for the bob? Is this because the bob is just treated as a point mass? What if the bob isn't treated as a point pass?

 

[erobz]

I didn't mean the total MoI, but just the one of the bob.
For the rod, as you described, the distance of an axis parallel to the axis of rotation is taken into account.
Why isn't this the case for the bob? Is this because the bob is just treated as a point mass? What if the bob isn't treated as a point pass?

You're asking where does the $mr^2$ seemingly disappear when considering the Energy, but it would be here in considering the Force? I don't know for sure. I "think" its already accounted for in the work definition through the dot product when considering energy?

$$ KE = \int \mathbf{\hat{F}} \cdot d\mathbf{\hat{r}} $$

 

[Baluncore]

The bob can be computed as a point mass at the end-pin of the rods.
If the bob was not a point mass, then it's CofM would be at the end-pin of the rods.

The bob does not rotate, so the bob does not have an angular velocity.
The bob has a linear velocity aligned with the tangent to the circular path of the rod end.

 

[Baluncore]

Is the Newton's Method necessary?

Probably not, if one can solve for ω².

 

[erobz]

The bob can be computed as a point mass at the end-pin of the rods.
If the bob was not a point mass, then it's CofM would be at the end-pin of the rods.

The bob does not rotate, so the bob does not have an angular velocity.
The bob has a linear velocity aligned with the tangent to the circular path of the rod end.

This is what is confusing to me. I think grvlfun also.

$\mathbf{ \hat{v_r}}$ and $\mathbf{ \hat{v_b}}$ are in the same direction throughout motion.

I would expect the total kinetic energy of the rod about $O$ to be:

$$ \frac{1}{2} \left( I_r + m_r \left( \frac{r}{2} \right)^2 \right) \left( \frac{r}{2} \right)^2 \omega^2 $$

By the same logic I would expect the total KE of the bob to be:

$$ \frac{1}{2} \left( m_b r^2 \right) r^2 \omega^2 $$

The bob is not rotating about its center of mass, but as a point mass it is still rotating about $O$?

You are seemingly saying this is completely wrong...and maybe it is...But I'm not personally understanding it.

EDIT:
I've made some goofy error, I didnt realize until I examined the units

$$ KE_{rod} = \frac{1}{2} \left( I_r + m_r \left( \frac{r}{2} \right)^2 \right) \omega^2 $$

and

$$ KE_{bob} = \frac{1}{2} \left( m_b r^2 \right) \omega^2 $$

 

[Baluncore]

You are seemingly saying this is completely wrong...and maybe it is...But I'm not personally understanding it.

As a point mass you can treat it either way.

What is the MofI of a rod rotating about an end point ?
I = m * L² / 3 ; which is not the centre of mass.

 

[erobz]

As a point mass you can treat it either way.

What is the MofI of a rod rotating about an end point ?
I = m * L² / 3 ; which is not the centre of mass.

What other way were you expecting it to be treated for the bob so I can perhaps reconcile my understanding?

$$ KE = \frac{1}{2} m_b \left( v_x^2 + v_y^2 \right) \neq \frac{1}{2}m_b r^4 \omega^2 $$

Because I can't get that to work if its what you had in mind for "KE_linear(bob)".

EDIT: goofy error correction

$$ KE_{bob} = \frac{1}{2} m_b \left( v_x^2 + v_y^2 \right) = \frac{1}{2}m_b r^2 \omega^2 $$

$$ \begin{align} \frac{1}{2} m_b \left( v_x^2 + v_y^2 \right) \tag*{} &= \\ &= \frac{1}{2} m_b \left( \left( v_b \cos \theta \right)^2 + \left( v_b \sin \theta \right)^2 \right) \tag*{} \\ &= \frac{1}{2} m_b v_b^2 \left( \cos^2 \theta + \sin^2 \theta \right) \tag*{} \\ &= \frac{1}{2} m_b v_b^2 \tag*{} \\ &= \frac{1}{2} m_b r^2 \omega^2 \tag*{} \end{align} $$

All is right with the world again...Sorry for any confusion I may have caused with the bogus result. I've added the Edits so it becomes apparent what I did incorrectly.

 

[grvlfun]

Thank you very much Baluncore and erobz !
If possible I would like to ask a further question, now that I am able to calculate the velocity.
The attachment on the linkage consists of 2 plates. An upper and a lower plate. The lower plate can move up and down freely. It is intended that the lower plate hits the ground before angle θ is 0 and is dragged over the ground by the motion of the pendulum.
How could I calculate the impact energy of the lower plate?

I don't expect the impact energy to be PE(initial)_rod + PE(initial)_bob, nor PE(initial)_bob alone, as not everything hits the ground.

 

[Baluncore]

At the instant of contact, you could separate the bob into two separate masses. But you have not specified if the impact is “backed” by the lower mass or by the original total bob mass. How are the two parts of the bob physically connected?

Toward the end of the swing I would expect you to be interested in the horizontal component of the contact, like you were launching a puck across a frozen lake. You have not specified if the direction of impact includes the horizontal and vertical components, against an unknown hard or soft surface, with or without friction.

 

[erobz]

"Impact energy" seems a little vague. Are you asking for impact Force maybe? This motion is starting to get more complex. I've personally never solved this typed of a problem, but I'd like to think about it.

I'm thinking that the bottom plate and the posts must be guided through the top plate as it continues to sink. Thus, the lowers acceleration in the y direction once it makes contact should be 0 over the duration of contact.

I would think you calculate the potential and kinetic energy just before impact. From there you apply Newtons Second Law in the vertical direction to a FBD of the lower assembly.

Assuming the posts are well lubricated:

$$ \uparrow^+ \sum F_y = N - m_l g = m_l \frac{dv_y}{dy} = 0 $$

In the meantime the energy that is dissipated while the lower portion is in contact with the surface is:

$$ \int F_{fr} \cdot dx = \int \mu N \cdot dx $$

So that the energy just after it begins to ascend is :

$$ KE( x) = KE(x') + \int_{x}^{x'} \mu m_lg \cdot dx $$

I'm not sure about this though. First round draft. likely overlooking something(s).

EDIT:
I'm already suspicious that the Normal Force doesn't have dependencies on the velocity $v_y$ when contact is initiated. When its initially contacting its has to undergo an acceleration in this direction until it reaches $v_y = 0$. I'm just not sure how to capture what it is in the EOM.

 

[grvlfun]

At the instant of contact, you could separate the bob into two separate masses. But you have not specified if the impact is “backed” by the lower mass or by the original total bob mass. How are the two parts of the bob physically connected?

Toward the end of the swing I would expect you to be interested in the horizontal component of the contact, like you were launching a puck across a frozen lake. You have not specified if the direction of impact includes the horizontal and vertical components, against an unknown hard or soft surface, with or without friction.

What do you mean by backed? The upper plate is fixed to the swinging rods. The lower plate is fixed via a linear rail system to the upper plate. So its only movement path is up and down (y axis), can't go left/right, front/back. I would say the impact is only backed by the lower mass and not the full bob mass.

Once the lower plate has hit the ground, it will be dragged over the ground until it is lifted off again due to the pendulum motion. After the initial impact, the second phase would be dragging: here, the mass of the lower plate exerts a certain pressure on the ground.
The hardness/softness of the ground vary and the friction coefficient varies as well, due to different materials used.

"Impact energy" seems a little vague. Are you asking for impact Force maybe? This motion is starting to get more complex. I've personally never solved this typed of a problem, but I'd like to think about it.

I actually just need the impact energy. Like from a free fall, where you let fall a steel ball onto something and its impact energy will be the potential/kinetic energy.
For the impact force as you stated I either need the displacement distance or the collision time. I don't have any of them and I may get to use a force plate to catch the impact forces.

I would think you calculate the potential and kinetic energy just before impact. From there you apply Newtons Second Law in the vertical direction to a FBD of the lower assembly.

Based on your answers I recognised that I simply missed the fact that KE = 0.5*m*v² and that one can split the linear velocity in v_x and v_y. I was thinking in the direction of using the acceleration of the bob point mass and then PE = m*a*h...

So, as I have the velocity, I will separate the bob into 2 masses, and calculate KE = 0.5*m_{lower mass}*v_x².

Question: The bob/attachment is treated as a point mass. With its size and v = r*ω, the lower mass has a certain distance to the end point of the rod. By separating the bob in 2 masses, should a change in the distance r be included or just kept the same distance of the point mass?

 

[erobz]

Question: The bob/attachment is treated as a point mass. With its size and v = r*ω, the lower mass has a certain distance to the end point of the rod. By separating the bob in 2 masses, should a change in the distance r be included or just kept the same distance of the point mass?

$r$ should be at the CoM of the bob, and the EOM change once the lower plate has contacted the ground (so there is no need to change that). The EOM for the bob once its sliding should be based on both the FDB of the bob and the FBD of the rod which are coupled through the contact force between the top plate and the bottom rods sliding through it as the bob is translating horizontally.

 

[Baluncore]

Question: The bob/attachment is treated as a point mass. With its size and v = r*ω, the lower mass has a certain distance to the end point of the rod. By separating the bob in 2 masses, should a change in the distance r be included or just kept the same distance of the point mass?

Since the bob does not rotate, it is the linear velocity along the circular path that is important, not the CofM. The height of the pendulum fulcrum should be selected so that the lower part of the bob contacts the surface at the appropriate rod -angle, then lifts off again at +angle.

The bottom of the bob will contact the surface before it slides along. The vertical velocity at that instant of contact is due to the velocity of the bob along the arc of the pendulum. The shorter the contact angle, and the softer the surface, the more gentle will be the impact.

Since the two parts of the bob are attached, the horizontal progress of the bob along the surface is driven by the angular momentum of the rod and the horizontal linear momentum along the arc of the total bob mass. That is what I meant by "backed" by the total mass.

The mechanism has three rods to keep the bob level. The model only has one rod to make computation tractable. I still don't know what is being engineered here.

 

[grvlfun]

The mechanism has three rods to keep the bob level. The model only has one rod to make computation tractable. I still don't know what is being engineered here.

The device should simulate an impact + sliding over a very short distance. The first idea was a pendulum with 1 rod, however this wouldn't keep the attachment level. Therefore the 4 bar 'parallel' linkage.
The 3 bars are a result of the construction: rod AD is mounted on the middle of the D axis of the attachment. BC consist of 2 rods mounted on each side of the attachment at axis C. Point B consists of 2 axes each side, not connected to each other, so rod AD can pass by once it's turned > 90°.

Like already said, the attachment consists of an upper and lower plate, with the lower plate being able to move up and down. By varying the distance between the 2 plates, one can vary the distance the lower plate is dragged over the ground. The same goes for the radius/length of the rods.
All in all its a tradeoff between velocity, impact energy and distance but for now it's the 'easiest' and most space saving method.

Thanks to your initial hints I recognised a design flaw with the twisting at >90°. I will try to make it a real parallel linkage, in order to eliminate the twisting and simplify the calculations.

I really appreciate your help and got a much better understanding of the physics behind it. I also understood now (at least I think so) why the bob is treated as a point mass and has linear movement.

 

[erobz]

Since the bob does not rotate, it is the linear velocity along the circular path that is important, not the CofM. The height of the pendulum fulcrum should be selected so that the lower part of the bob contacts the surface at the appropriate rod -angle, then lifts off again at +angle.

The bottom of the bob will contact the surface before it slides along. The vertical velocity at that instant of contact is due to the velocity of the bob along the arc of the pendulum. The shorter the contact angle, and the softer the surface, the more gentle will be the impact.

Since the two parts of the bob are attached, the horizontal progress of the bob along the surface is driven by the angular momentum of the rod and the horizontal linear momentum along the arc of the total bob mass. That is what I meant by "backed" by the total mass.

The mechanism has three rods to keep the bob level. The model only has one rod to make computation tractable. I still don't know what is being engineered here.

How do you account for the first stage of the impact? I can't seem to figure out how to capture it in the model.

Beginning at the point of impact:

$$ \sum F_y = N - mg = m \frac{dv_y}{dt} $$

Clearly, there must be a non-zero acceleration $\frac{dv_y}{dt}$ for some ( probably brief period ), until $v_y = 0$. I know its the impulse curve, but it has occurred to me that "how to model it" is a black box in my understanding.

 

[Baluncore]

I know its the impulse curve, but it has occurred to me that "how to model it" is a black box in my understanding.

There will be an energy reduction due to the loss of vertical KE for the lower-bob mass. Apart from that we would need to know the materials involved, and the reason for this analysis.
Will the lower-bob mass bounce ?
How deformable is the surface ?

 

[erobz]

Apart from that we would need to know the materials involved, and the reason for this analysis.
Will the lower-bob mass bounce?

I don't personally care for the reason, I'm just curious about the result. What is the simplest model that attempts to account for this energy loss?

 

[Baluncore]

The vertical KE component generates a sound wave in the ground, then the pendulum is stopped by friction with the ground. Or if the ground is a slab of ice, continues on without friction, lifts off again and repeats.

 

[erobz]

The vertical KE component generates a sound wave in the ground, then the pendulum is stopped by friction with the ground. Or if the ground is a slab of ice, continues on without friction, lifts off again and repeats.

I'm only interested in the "sound wave" part. The "possible" stopping by friction is commonly described (I've already written out the EOM for that part of the motion I believe).

What I'm interested in: How does the sound wave manifest in the equations of motion?

 

[Baluncore]

What I'm interested in: How does the sound wave manifest in the equations of motion?

The EoM of the lower bob, or of the ground ?
There is no simple way to guess the characteristics of the ground material.
Different materials will necessitate different models.
It is possible to over-extend a model.

I would be more interested in how the mechanism could operate above 90° with the three rods suggested.
I would design it with one link on either side of the bob, with a chain or stepped belt and two equal sized sprockets, so the bob would remain horizontal while it passes over the top without tangling it's rods. That also eliminates the problem of parallel link length and clearance as the bob is passing 90°.