Four Charges In a square (Electric Fields)

[Noisuf]

Homework Statement

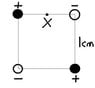
Four charges are arranged in a square. 2 Positive and 2 negative, in opposite corners. The magnitude is |1.6x10^-6 C|. The square's sides are 1 cm. A] At point X (Midpoint of of one of the sides. See Picture) Find the electric field direction and magnitude. B] What is the force of an electron at point X. C] What is the force on an electron that is very far away from the four poles.

Homework Equations

E=(Kq)/r^2 F=qE

The Attempt at a Solution

For A I know the electric field for all for points using the first equation. But at that point i don't know how to add them using vectors and what not. I added the top 2 and got 8.9X10^7. But I know the bottom two do something to the point, but i don't know what.

For B i know how to find once i have the field quantity. Just multiply it by the charge of the electron.

For C I guess my teacher means at infinity, therefore the field is 0. and with equation 2 makes the force 0, and making it an equilibrium.

Thanks for any help.

 

[chrisk]

Resolve each E vector from each charge at point X into horizontal and vertical components then add the components to get the net components. Use the net components to find the magnitude and direction.

 

[Noisuf]

Ok after trying this and thinking of it like that don't the top 2 cancel out? and I am not sure how to add in the bottom two vector wise. The bottom twos vectors meet at point x in a equal in magnitude but opposite in direction, why does that not cancel out?

 

[Gokul43201]

Since the picture is not visible yet, it would help if you first clarified some positions.

Top-left = + or - ?
Top-right = + or - ?
Bot-left = + or - ?
Bot-right = + or - ?

X = top or bot or left or right?

 

[Noisuf]

top left +
top right -
bottom left -
bottom right +

x is mid point of top two

 

[Gokul43201]

Do this one charge at a time.

You have calculated the field at X due to the + charge at the top left (TL)?

What is its magnitude and direction? How would you draw the vector representing this field at point X?

 

[Noisuf]

Ok for the top left (+) I have calculated a field E=k(1.6x10^-6)/(.005m)= 5.696x10^8 N/C
This vector is pointing towards X. For the negative in the top. The quantity is negative same math. -5.696x10^8 N/C. The vector is going away. Adding these 2 = 0? or do you just add the magnitude. Then its 1.1x10^9 N/C. The bottom two still don't make any sense. The vector points away from the positive toward x, and for the negative, x points toward it. In the horizontal components are the same as the top, but in reverse. The vertical components will use the radius 1cm, but still they are opposite in direction so cancel out? I'm not very good with vectors :(

 

[Gokul43201]

I can only recommend that you properly learn how to resolve vectors and find the resultant (sum) of several vectors by means of vector resolution. This should be covered in the early part of your physics textbook (probably from a previous class on mechanics).

 

[Noisuf]

Ok I have reviewed vector addition and I am coming up with 1.37x10^-7 N/C Pointing up from X. If anyone has worked this problem, can anyone confirm.

 

[Gokul43201]

Sorry for the delay.

I haven't checked the numbers on this but:

1. The resultant does not point upwards - you must be making a mistake.
2. In the top line of post #7, it appears you forgot to square the distance in the denominator.

If you still have time for this, fill in the magnitudes and directions for each of the 4 fields due to the charges located in the 4 corners (TL, TR, BL, BR):

E(TL) =
E(TR) =
E(BL) =
E(BR) =

Next, you need to resolve these into their horizontal (x) and vertical (y) components.

E(TL,x) =
E(TL,y) =

E(TR,x) =
E(TR,y) =

E(BL,x) =
E(BL,y) =

E(BR,x) =
E(BR,y) =