Four-vectors and related concepts

[Austin0]

=DrGreg;2312738]Yes, the concept of parallel lines works just as well in Minkowski spacetime as in does in Euclidean space. And switching from one inertial frame to another doesn't affect parallelism.

then the similarity is true even in the Euclidean geometry of the paper you draw it on, but (I think) it's also true in some sense in Minkowski geometry too.

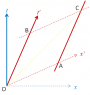
Thanks for taking the time to do the drawing. I did a rough sketch of the similarity i was referring to.
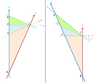
In it one triangle is [A,O ,C] the x' of S' and the (t ,x )axi of S

The other is [B,O,C ] the t' of S' and (t , x )axi of S



The ratio of the length of B,C to O,B is equivalent to the ratio of A,C to O,C
This equivalence is geometrically direct but quantitatively requires the transformation.
One is a time measure and one a distance measure.

A vertical flip of [A,O,C] and extending the hypotenuse makes another valid line of simultaneity or synchronicity.

WHy is it that this is never mentioned or incorporated into the system??
Or is it that I have just never encountered it?

In Minkowski space is there a difference between applying the trig functions directly and then transforming the results and using functions that incorporate the transform?

How about "gravitational time dilation"? In relativity we don't distinguish between the "true" gravity due to matter and the "pseudo-gravity" of acceleration, it's all just "gravity".

Alright.
BTW I appreciated your, as you put it "pedantic" correction of the misuse of the term parabola in that other thread about Minkowski diagrams. I had been very confused and had actually searched the web for references because I didnt know what they were talking about

In the context of relativity, "flat" and "Euclidean" aren't the same thing at all Minkowski geometry isn't Euclidean geometry, but it's still "flat". That's because (sticking to our simplified 2D spacetime) we can draw spacetime diagrams on a flat piece of paper. This is a bit of an oversimplification, but if spacetime is curved, you have to draw the diagram on a curved surface, such as the surface of a sphere. If you use curved gridlines on a flat surface, it's still flat spacetime, and the geometry hasn't changed, just the coordinate system

.

This is a bit of a semantically elusive subject here. In the context of spacetime as being the real world space then isn't SR spacetime both flat and Euclidean? Inertial straight lines etc.?
Obviously 2D drawings are flat but isn't the spacetime represented by the drawings also flat as just described ??
Don't those curved gridlines then represent a real world spacetime that is no longer either flat nor EUclidean? SO the drawing may be "flat" but the spacetime isn't??

R[/IAll valid coordinate systems must make identical predictions about anything that you can measure that isn't just a feature of the coordinates themselves. For example whether or not two particles collide, or how much time will elapse on a single clock transported between two events. The equations that describe the laws of physics may change when you switch between different coordinate systems (but not between two Minkowski coordinate systems in the absence of gravity). And some coordinate systems may not extend to the whole of spacetime, they may only be valid within a restricted region.

Say we take measurements of the paths of two particles over a short distance in an Earth lab. They are parallel as measured. We plot those paths in a cartesian 4D frame and a GR frame. Am I correct in thinking that within a sufficiently small subsector of space that GR space is basically Euclidean and that the coordinate paths would be virtually identical?
But the extrapolation [not further measurement] within the two systems would be very different. That to have correspondence would require the introduction of gravity into the cartesian system. This is implicit in the GR coordinate system , just as the gamma factor is implicit in the Lorentzian system.
But in the Cartesian space it is a necessary added assumption. SO that is part of my enquiry; Is curved space intrinsic in Minkowski space , derivable directly from the postulates and math of SR or is it an imported assumption.
This is all tied in with several other questions as well as the basic desire to really understand the geometry of the system. That is why I am trying to fit in hyperbolas and see how they relate and if they also suggest curvature in some way when in the context of two purely inertial frames , with no acceleration involved. SO far I have encountered the hyperbolas of invarience and some ways they relate to the relative values within the space
but not yet how they directly apply in the direct geometrically spatial way that ellipsoids do.
I just realized I am rambling on here.
Thanks for your help , I hope I don't overextend your legendary patience

 

[DrGreg]

In it one triangle is [A,O ,C] the x' of S' and the (t ,x )axi of S
The other is [B,O,C ] the t' of S' and (t , x )axi of S

Sorry, I'm not understanding this. In particular, what event you mean by "(t ,x )axi of S".

Attached is my guess. Is that what you meant?

This is a bit of a semantically elusive subject here. In the context of spacetime as being the real world space then isn't SR spacetime both flat and Euclidean? Inertial straight lines etc.?
Obviously 2D drawings are flat but isn't the spacetime represented by the drawings also flat as just described ??
Don't those curved gridlines then represent a real world spacetime that is no longer either flat nor EUclidean? SO the drawing may be "flat" but the spacetime isn't??

I need to make clearer the distinction between "Euclidean geometry" and "Minkowski geometry"

In an N-dimensional Euclidean geometry, it is possible to choose coordinates so that the metric is given by

$$ds^2 = dx_1^2 + dx_2^2 + ... + dx_N^2$$​

In 4-dimensional Minkowski geometry, it is possible to choose coordinates so that the metric is given by

$$ds^2 = dt^2 - dx^2 - dy^2 - dz^2$$​

In special relativity (i.e. no gravity) the geometry of 4D spacetime is always Minkowski, but the geometry of 3D space is always Euclidean.

"Straight lines" are technically called "geodesics". The defining property of a geodesic is that it has the shortest or longest "distance" between two events in spacetime, "distance" being defined by the metric "ds". (In general relativity we need to add the word "locally".) It's a fundamental assumption of the mathematical model of relativity that the worldlines of free-falling objects are geodesics.

In standard Minkowski (t,x,y,z) coordinates (without gravity), geodesics have simple linear equations like $x=x_0+v_xt$, $y=y_0+v_yt$, $z=z_0+v_zt$. In other "curved coordinates" (i.e. non-inertial frames) the geodesics have more complicated equations, but they are still the same lines in spacetime.

The concept of "spacetime" is independent of the choice of coordinates (frame) you use to measure the events. Think of spacetime as a blank sheet of paper, and think of a coordinate system, or frame, as a set of gridlines that you draw on the paper. If the paper is flat, spacetime is "flat" and there's no gravity. (Here, I mean "gravity" in the Newtonian sense and I exclude the pseudo-gravity of an accelerating frame, which corresponds to curved gridlines on flat paper.)

The weight that you feel when stood still on Earth or when you're in an accelerating rocket is due to your wordline not being a geodesic, i.e. not as straight as it could be on the "paper", whether or not the paper is curved. Curved spacetime gives rise to "tidal effects", the most obvious being that two "straight" lines drawn on curved sheet may begin parallel but may converge or diverge further along. (E.g. like lines of longitude on a globe.)

That is why I am trying to fit in hyperbolas and see how they relate and if they also suggest curvature in some way when in the context of two purely inertial frames , with no acceleration involved. SO far I have encountered the hyperbolas of invarience and some ways they relate to the relative values within the space
but not yet how they directly apply in the direct geometrically spatial way that ellipsoids do.

Hyperbolas are to Minkowski geometry what circles are to Euclidean geometry, in two dimensions. That's why they crop up so often in relativity. (In more dimensions, it's hyperboloids and spheres.)

Thanks for your help , I hope I don't overextend your legendary patience

I'm not sure about this legend. Perhaps I should explode with rage to dispel it.

 

[Dale]

The concept of "spacetime" is independent of the choice of coordinates (frame) you use to measure the events.

Austin0, this sentence of DrGreg's is incredibly important! This is the reason that spacetime, four-vectors, and Minkowski geometry are so important. It allows relativity to be formulated in terms of geometric objects which are themselves independent of the particular coordinate system used (in the same way that a traditional vector is a geometric object which is independent of the coordinates in which it is expressed).

 

[Austin0]

=DrGreg;2315609]Sorry, I'm not understanding this. In particular, what event you mean by "(t ,x )axi of S".

Sorry,once again foiled by language [my ineptness with]. I incorrectly wrote axi instead of axes. SO there is no specific event . What I am talking about is a general relationship like lines of simultaneity that apply to any point of time. Attached drawing.[forgive the crudeness, my photoshop is going south on me , no text tool]

This is four takes on a single diagram. The basic diagram being #4
#1 (blue triangle) being similar to #2 (orange triangle) being congruent to #3(yellow triangle)
That the trig functions relevant to similarity apply but need the tranformation factor.
The line K in #3 is the second line of synchronicity I was referring to;

original austin0 A vertical flip of [A,O,C] and extending the hypotenuse makes another valid line of simultaneity or synchronicity.

WHy is it that this is never mentioned or incorporated into the system??
Or is it that I have just never encountered it?

I need to make clearer the distinction between "Euclidean geometry" and "Minkowski geometry"

In an N-dimensional Euclidean geometry, it is possible to choose coordinates so that the metric is given by

$$ds^2 = dx_1^2 + dx_2^2 + ... + dx_N^2$$​

In 4-dimensional Minkowski geometry, it is possible to choose coordinates so that the metric is given by

$$ds^2 = dt^2 - dx^2 - dy^2 - dz^2$$​

My memory is terrible but i think I remember 4D Cartesian coordinates expressed as

$$ds^2 = dt^2 + dx^2 + dy^2 + dz^2$$​

?
When you say geometry in this context you mean Pythagorean trigonometry applied to kinematics correct?

In special relativity (i.e. no gravity) the geometry of 4D spacetime is always Minkowski, but the geometry of 3D space is always Euclidean.

Isn't it correct that the real difference in the Lorentz math in this context is temporal??
That clock desynchronization is implicit in the math. Uniform clock desynch in itself does not change the linearity of measured particle paths. That straight lines still tranform as straight lines? But differential dilation of clocks does in fact inevitably introduce curved paths??

The concept of "spacetime" is independent of the choice of coordinates (frame) you use to measure the events. Think of spacetime as a blank sheet of paper, and think of a coordinate system, or frame, as a set of gridlines that you draw on the paper. If the paper is flat, spacetime is "flat" and there's no gravity. (Here, I mean "gravity" in the Newtonian sense and I exclude the pseudo-gravity of an accelerating frame, which corresponds to curved gridlines on flat paper.)

original austin0 _______________________________________________________________
In the context of spacetime as being the real world space then isn't SR spacetime both flat and Euclidean? Inertial straight lines etc.?
Obviously 2D drawings are flat but isn't the spacetime represented by the drawings also flat as just described ??
Don't those curved gridlines then represent a real world spacetime that is no longer either flat nor EUclidean? SO the drawing may be "flat" but the spacetime isn't??

The weight that you feel when stood still on Earth or when you're in an accelerating rocket is due to your wordline not being a geodesic, i.e. not as straight as it could be on the "paper", whether or not the paper is curved. Curved spacetime gives rise to "tidal effects", the most obvious being that two "straight" lines drawn on curved sheet may begin parallel but may converge or diverge further along. (E.g. like lines of longitude on a globe.)

austin0___________________________________________________________________
""Say we take measurements of the paths of two particles over a short distance in an Earth lab. They are parallel as measured. We plot those paths in a Cartesian 4D frame and a GR frame. Am I correct in thinking that within a sufficiently small subsector of space that GR space is basically Euclidean and that the coordinate paths would be virtually identical?
But the extrapolation [not further measurement] within the two systems would be very different.""

Hyperbolas are to Minkowski geometry what circles are to Euclidean geometry, in two dimensions. That's why they crop up so often in relativity. (In more dimensions, it's hyperboloids and spheres.)

Hyperboloids not ellipsoids? DO hyperboloids turn up because they are intrinsic geometry or because they outline the surface of an ellipsoid in a complementary way or because the Lorentz math itself describes a hyperbolic curve and that graphs of other expressions of the fundamental gamma function contraction etc reflect this?

I'm not sure about this legend. Perhaps I should explode with rage to dispel it

If you decide to test this hypothetical I just hope you don't do it with me
Thanks

 

[DrGreg]

This is four takes on a single diagram. The basic diagram being #4
#1 (blue triangle) being similar to #2 (orange triangle) being congruent to #3(yellow triangle)
That the trig functions relevant to similarity apply but need the tranformation factor.
The line K in #3 is the second line of synchronicity I was referring to;

original austin0 A vertical flip of [A,O,C] and extending the hypotenuse makes another valid line of simultaneity or synchronicity.

WHy is it that this is never mentioned or incorporated into the system??
Or is it that I have just never encountered it?

OK, I've redrawn the diagram which is attached. First look at the left-hand diagram only.

Yes, AOC is similar to COB. And you can draw KOC congruent to AOC but it doesn't have much significance.

OC is a line of simultaneity for the blue (t,x) observer.
AC is a line of simultaneity for the red (t',x') observer.
KC isn't a line of simultaneity for either of them. In fact it would be a line of simultaneity for a third observer who, relative to the blue observer, is traveling with an equal-but-opposite velocity to the red observer.

The right hand diagram depicts exactly the same thing from the red observer's point of view. Although in Euclidean geometry the two diagrams look quite different, in Minkowksi geometry (or hyperbolic geometry) the two diagrams are virtually identical, the only difference being that one has been "rotated", in a Minkowski-geometry sense, relative to the other.

Both diagrams depict exactly the same spacetime, just "viewed at two different angles".

My memory is terrible but i think I remember 4D Cartesian coordinates expressed as

$$ds^2 = dt^2 + dx^2 + dy^2 + dz^2$$​

?
When you say geometry in this context you mean Pythagorean trigonometry applied to kinematics correct?

Er, in Newtonian physics, time doesn't come into it. Measurements in space are given by the Euclidean metric

$$ds^2 = dx^2 + dy^2 + dz^2$$​

Measurements in time are given by

$$d\tau^2 = dt^2$$​

It's only in relativity that we combine the two to get the Minkowski metric

$$ds^2 = dt^2 - dx^2 - dy^2 - dz^2$$​

In relativity, when we speak of "geometry" we are usually referring to spacetime rather than space alone. It's an analogy: we apply geometrical concepts such as parallel lines, length and angle to the "worldlines" and "lines" or "planes" of simultaneity in spacetime. The mathematical description of spacetime geometry is very similar to the mathematical description of ordinary space geometry, but with a different metric. That's why we call it "geometry".

Isn't it correct that the real difference in the Lorentz math in this context is temporal??
That clock desynchronization is implicit in the math. Uniform clock desynch in itself does not change the linearity of measured particle paths. That straight lines still tranform as straight lines? But differential dilation of clocks does in fact inevitably introduce curved paths??

But even in Newtonian physics, where there is absolute time and never any dilation, an accelerating observer would see an inertial object moving along an apparently curved path relative to himself, so dilation and apparent curvature relative to your grid are two separate issues.

(Note I say "apparent curvature" because if, in relativity, you measure curvature in the mathematically correct way, taking account of your own coordinate system and the equation for the metric in those coordinates, then inertial paths still have zero curvature, even though they might not look like it. But the maths of this is advanced stuff, involving tensors.)

Hyperboloids not ellipsoids? DO hyperboloids turn up because they are intrinsic geometry or because they outline the surface of an ellipsoid in a complementary way or because the Lorentz math itself describes a hyperbolic curve and that graphs of other expressions of the fundamental gamma function contraction etc reflect this?

Hyperboloids are the 3D surfaces in 4D space time that are a constant spacetime interval (=the "pseudo-distance" of spacetime) from an event, e.g. given by

$$c^2t^2 - x^2 - y^2 - z^2 = a^2$$​

for some constant a. A vertical 2D slice through it would be a hyperbola; a horizontal 2D slice would be a circle.

 

[Austin0]

=DrGreg;2318843]OK, I've redrawn the diagram which is attached. First look at the left-hand diagram only.

Yes, AOC is similar to COB. And you can draw KOC congruent to AOC but it doesn't have much significance.

OC is a line of simultaneity for the blue (t,x) observer.
AC is a line of simultaneity for the red (t',x') observer.
KC isn't a line of simultaneity for either of them. In fact it would be a line of simultaneity for a third observer who, relative to the blue observer, is traveling with an equal-but-opposite velocity to the red observer.

Using your drawing.
I will just give my interpretation of lines of simultaneity and you can correct me where neccessary.
If we consider point O as being both x=0 and t=O (not zero) and t'at C being t'=C

Location A, (x=0,t=A) ,,,[ the intersection of red's line of Simultaneity and the timeline of blue frame at x=0 ], represents the colocation of a (hypothetical or real ) observer and clock or just a clock in red's frame ,,with the observer and clock at x=0 in blues frame ,at the point when that red observers proper time reading was the same as the time reading of the clock at point C in reds frame (x'=A ,t'=C) ,(x'=C,t'=C).. and the clock in blue was reading the value indicated by that point on the timeline. (x=0,t=A), (x'=A ,t'=C)

Line A C graphs the spatial location of the observer or clock in Red frame. It has the same spatial relationship to line O C as the temporal relationship between the length of the lines BC and OB.

That this is true at any point along the world lines or any point along the line of simultaneity. This is an accurate graph depicting the relationship between clock readings (colocation events) at any spacetime point in either frame. A complete and unique set of [(x,t),(x',t')]

Line KC graphs the exact same set of events. Every particular (x,t),( x',t') tuple found on AC is also found on KC. Point A depicts the time of the clock in S ,at x=0 according to the simultaneity of S' Point K depicts the reading on the colocated clock in S' according to the simultaneity of S (at t=O not 0).
Line KC graphs the spatial location of that clock in x' as observed in S at t=O.

SO --1) ( x=0 ,t= O) is simultaneous with (x'= K, t'=K).
2) (x=0, t=A) is simultaneous with (x'=A, t'= C)
3) (x=C, t=O) is simultaneous with (x'=C, t'=C )

This is an objective reality that both frames agree on.

But IMO 4) (x=0,t=O) is not simultaneous with (x'=C, t'=C)
5) (x'=C,t'=C) is not simultaneous with (x'=A,t'=C),(x=0,t=A)
6) (x'=C,t'=C) is not simultaneous with (x'=K,t'=K),(x=0,t=0)

There is no possible agreement between frames here so any assumption of simultaneity is to choose a preferred frame.

To my understanding that was the essential point of the Relativity of Simultaneity.
So this is just my understanding and I realize I may be wrong on any or all points. If the description is too confusing using these drawings I will do a set with actual values.

Er, in Newtonian physics, time doesn't come into it. Measurements in space are given by the Euclidean metric

$$ds^2 = dx^2 + dy^2 + dz^2$$​

Measurements in time are given by

$$d\tau^2 = dt^2$$​

It's only in relativity that we combine the two to get the Minkowski metric

$$ds^2 = dt^2 - dx^2 - dy^2 - dz^2$$​

In relativity, when we speak of "geometry" we are usually referring to spacetime rather than space alone. It's an analogy: we apply geometrical concepts such as parallel lines, length and angle to the "worldlines" and "lines" or "planes" of simultaneity in spacetime. The mathematical description of spacetime geometry is very similar to the mathematical description of ordinary space geometry, but with a different metric. That's why we call it "geometry".

How can you have physics, particularly mechanics without time?
Wouldn't any actual application of kinematics [ bouncing ball ,whatever] that was charted in cartesian space naturally include time?
Doesnt the Galilean transform contain a time factor??
I think this may be getting into a semantic swamp here.

But even in Newtonian physics, where there is absolute time and never any dilation, an accelerating observer would see an inertial object moving along an apparently curved path relative to himself, so dilation and apparent curvature relative to your grid are two separate issues

.

Agreed but in Newtonian physics there would be no assumption that the curvature was integral to space itself. That is exactly the interpretation applied to accelerating systems with Rindler coordinates.
Agreed also that dilation and curvature are two separate issues except they go hand and hand in Rindler coordinates don't they?.
Part of my motivation for this enquiry is; I encountered in another thread, the assertion that the dilation and curvature in an accerating frame could be derived purely from first principles with no additional assumptions. I.e. The fundamental postulates and Lorentz math as applied in Minkowski space.
I didnt see this but I did not reject it out of hand , I set out to find out as much as I could on the subject. So far, it appears to me that the fundamental Minkowski space is flat and Euclidean and that the dilation and curvature are implicit in the imported Rindler coordinates. Certainly the gravitational dilation is right there in the basic functions you posted to me earlier. So if it is there in first principles I am just not getting it and maybe should just put it off until I have more math.

( Hyperboloids are the 3D surfaces in 4D space time that are a constant spacetime interval (=the "pseudo-distance" of spacetime) from an event, e.g. given by

$$c^2t^2 - x^2 - y^2 - z^2 = a^2$$​

for some constant a. A vertical 2D slice through it would be a hyperbola; a horizontal 2D slice would be a circle

I myself stumbled on the ellipsoid long ago, simply through contemplation of the simultaneity train. Picturing the track observer central to a sphere of brief fireworks , a quick flash of small points which he would perceive as a single event. Then imagining ,from the track point of view, the same occurance happening on the train. Where the points would start at the rear and proceed forward to the front while the observer was moving.
It seemed sure that the geometry was ellipsoid ,so I concluded that a sphere in one frame was extended through time to become an ellipsoid in another frame.
I also assume that the observer is located at one locus at the beginning and at the other locus when perceiving the flash but have never sat down to really work it out.
Wouldn't these be a " 3D surfaces in 4D space time that are a constant spacetime interval (=the "pseudo-distance" of spacetime) from an event" ?
So I am trying to equate this with the hyperbola.

Well thanks again

 

[Austin0]

=DrGreg;2318843]OK, I've redrawn the diagram which is attached. First look at the left-hand diagram only.

HI It has occurred to me that there may have been areas of ambiguity in my description.
It also seems like there is a much more direct approach through logic and fundamental principles.
So when I said complete and unique set of events I was not referring to simply the specific point in the timeline under consideration but the set of events extending backward and forward in time.
That as the two frames pass by each other; for any given specific point x in one frame and any point x' in the other frame there will be a singular colocation event. With a definite time on both clocks. The complete log for all points and times in the frames comprises the set i was referring to.
So if the point K in the line CK is a valid indication of the time relation between (x=0,t=O) and (x'=K,t'=K) and represents a valid colocation event. (x=0,t=O), (x'=K,t'=K) then it by principle must also be found on some line AC. Because observers must, by principle, always agree on local [co-local] events and the complete set of all such events must be singular and apply to both frames. SO does this clarify things and/or make any sense?

In relativity, when we speak of "geometry" we are usually referring to spacetime rather than space alone. It's an analogy: we apply geometrical concepts such as parallel lines, length and angle to the "worldlines" and "lines" or "planes" of simultaneity in spacetime. The mathematical description of spacetime geometry is very similar to the mathematical description of ordinary space geometry, but with a different metric. That's why we call it "geometry".

I think this also is an area where there is much room for confusion.
There is the geometry [and math] of; spacetime as meaning the real world.
There is the geometry and math of spacetime within the Minkowski spacetime [analog] that applies directly to the real world.
There is the geometry and math that applies to the analog itself as a 2D representation
with its necessary conventions due to the limitations of a flat piece of paper.
I.e. "length and angle in the worldlines" , parallel lines etc.

?

Thanks

 

[DrGreg]

Sorry, Austin0, I haven't had time to answer you yet. Finding the right words to answer to your questions requires some thought, which takes time. I will reply soon.

 

[Austin0]

Sorry, Austin0, I haven't had time to answer you yet. Finding the right words to answer to your questions requires some thought, which takes time. I will reply soon.

DrGreg Not at all a problem, I appreciate the time have you spent with me.
Regarding tthe second line of simultaneity question; It has only been recently that I have really gotten into the Minkowski diagrams . I have always used pairs of scaled linear diagrams as I found it easier to work with explicit contraction and desynchronization.
So I saw this other line of simultaneity. Played with it for a bit to check it out and a half hour later, filed it under interesting, and promtly forgot it. I never gave it a thorough workout as I had no idea of presenting it to anyone. So it just sort of slipped out when this discussion veered into Minkowski geometry. So I think you should not spend any of your time on it now. I will do some diagrams with actual values to check the idea and then if I wasn't having a brain lapse that day, I will send it to you in a clear easily, perused form.
Thanks again for all your help

 

[Austin0]

Sorry, Austin0, I haven't had time to answer you yet. Finding the right words to answer to your questions requires some thought, which takes time. I will reply soon.

Hi DrGreg I had to take a trip, I haven't forgotten.
Well I resolved or maybe more correctly dissolved the "other" line of simultaneity.
It turned out to be a bit of coincidence and a bit of sloppiness on my part.
When I started to explore the lines of simultaneity ,figuring out real values . as per habit I used a v=.8c system to work with. In this case by a fluke , the values for t',x' at the intersection of the rest system's lines of simultaneity and any position x ,do plot correctly as per the congruent hypotenuse I outlined. Or at least correctly enough I attributed a tiny deviation to round off error from doing the calcs by hand .
But now I have tried it with a range of relative v's it is obvious it was just coincidence and is not even close for other velocities.I know , DO the math!.
So I am glad to have disabused myself of that fallacy.
Attached are the diagrams just for amusement.

The question still remains whether I am correct in thinking that the lines of simultaneity, do ,in fact, correctly chart the relationship [degree of desynchronization between systems]
of specific clocks at specific locations [all locations and times] throughtout the timeline?

Er, in Newtonian physics, time doesn't come into it. Measurements in space are given by the Euclidean metric

It's only in relativity that we combine the two to get the Minkowski metric

In relativity, when we speak of "geometry" we are usually referring to spacetime rather than space alone. It's an analogy: we apply geometrical concepts such as parallel lines, length and angle to the "worldlines" and "lines" or "planes" of simultaneity in spacetime. The mathematical description of spacetime geometry is very similar to the mathematical description of ordinary space geometry, but with a different metric. That's why we call it "geometry".

How can you have physics, particularly mechanics without time?
Wouldn't any actual application of kinematics [ bouncing ball ,whatever] that was charted in Cartesian space naturally include time?
Doesnt the Galilean transform contain a time factor??
I think this may be getting into a semantic swamp here.

Aren't there actually two distinct "geometries" here. The geometry of spacetime meaning "the real world" and the math used within Minkowski space that applies directly to the real world. And the geometry that applies strictly within Minkowski space and the conventions that are in operation there. ?
Eg. ""as parallel lines, length and angle to the "worldlines" and "lines" or "planes" of simultaneity ""

But even in Newtonian physics, where there is absolute time and never any dilation, an accelerating observer would see an inertial object moving along an apparently curved path relative to himself, so dilation and apparent curvature relative to your grid are two separate issues

.

Agreed but in Newtonian physics there would be no assumption that the curvature was integral to space itself. That is exactly the interpretation applied to accelerating systems with Rindler coordinates.
Agreed also that dilation and curvature are two separate issues except they go hand and hand in Rindler coordinates don't they?.
Part of my motivation for this enquiry is; I encountered in another thread, the assertion that the dilation and curvature in an accerating frame could be derived purely from first principles with no additional assumptions. I.e. The fundamental postulates and Lorentz math as applied in Minkowski space.
I didnt see this but I did not reject it out of hand , I set out to find out as much as I could on the subject. So far, it appears to me that the fundamental Minkowski space is flat and Euclidean and that the dilation and curvature are implicit in the imported Rindler coordinates. Certainly the gravitational dilation is right there in the basic functions you posted to me earlier. So if it is there in first principles I am just not getting it and maybe should just put it off until I have more math.

( Hyperboloids are the 3D surfaces in 4D space time that are a constant spacetime interval (=the "pseudo-distance" of spacetime) from an event, e.g. given by

for some constant a. A vertical 2D slice through it would be a hyperbola; a horizontal 2D slice would be a circle

Picturing the track observer central to a sphere of brief fireworks , a quick flash of small points which he would perceive as a single event. Then imagining ,from the track point of view, the same occurance happening on the train. Where the points would start at the rear and proceed forward to the front while the observer was moving.
It seemed sure that the geometry was ellipsoid ,so I concluded that a sphere in one frame was extended through time to become an ellipsoid in another frame.?
I also assume that the observer is located at one locus at the beginning and at the other locus when perceiving the flash but have never sat down to really work it out.
Wouldn't these be a " 3D surfaces in 4D space time that are a constant spacetime interval (=the "pseudo-distance" of spacetime) from an event" ?
So I am trying to equate this with the hyperbola. And figure out if the hyperbola relates to the geometry of the real world or to Minkowski slices of that world , where light spheres are light cones etc.?

Well thanks again

 

[DrGreg]

The question still remains whether I am correct in thinking that the lines of simultaneity, do ,in fact, correctly chart the relationship (degree of desynchronization between systems) of specific clocks at specific locations [all locations and times] throughtout the timeline?

The lines of simultaneity tell you how an observer compares one clock against another. To compare two clocks you need to read both simultaneously, then a short while later read both simultaneously again. Divide one clock's time difference by the other's to calculate their relative rates. If there are any accelerations involved, by either of the clocks or by the observer, you need to consider the limit as the time difference tends to zero. "Simultaneously" is defined by the lines of simultaneity.

Thus the answer you get depends not only on the motion of the two clocks, but also on what you choose to be your lines of simultaneity. For inertial observers the standard choice is defined by Einstein's synchronisation convention. For non-inertial observers there are many choices available; one frequent choice is to use the lines of simultaneity of co-moving inertial observers, but other choices are available too.

When you set up a coordinate system, the t coordinate reflects the choice of synchronisation. Two events with the same t coordinate are simultaneous, in that system. It is usual to synchronise the t coordinate to the observer's own clock. But time measured by any other clock ("proper time") could go faster or slower than the t coordinate ("coordinate time"), in general.

I've used the phrase "line of simultaneity" above, but when you add in all the dimensions it should really be "plane of simultaneity". In 4D spacetime it's 3D hyperplane of simultaneity.

How can you have physics, particularly mechanics without time?
Wouldn't any actual application of kinematics (bouncing ball ,whatever) that was charted in Cartesian space naturally include time?
Doesnt the Galilean transform contain a time factor??
I think this may be getting into a semantic swamp here.

Aren't there actually two distinct "geometries" here. The geometry of spacetime meaning "the real world" and the math used within Minkowski space that applies directly to the real world. And the geometry that applies strictly within Minkowski space and the conventions that are in operation there. ?
Eg. ""as parallel lines, length and angle to the "worldlines" and "lines" or "planes" of simultaneity ""

Well, of course time comes into Newtonian physics, but it doesn't act as dimension of Euclidean geometry. In Newtonian physics there is only one time (apart from a trivial addition of a constant). The Galilean transform for time is just t' = t.

Don't get confused by the geometry of (3D) space and the geometry of (4D) spacetime. As 4 dimensions are hard to picture, let's lose one dimension and consider 3D spacetime and 2D space. With the usual convention of vertical time, spacetime consists of lots of geometrically identical horizontal Euclidean 2D spaces stacked on top of each other to form a 3D spacetime.

In the Newtonian/Galilean picture you can slide these spaces horizontally over each other, but that's it. You can measure distance within each slice (via ds² = dx² + dy²). You can measure time between slices (via $d\tau^2 = dt^2$). But you can't mix space and time. The slices are the planes of simultaneity (as we discussed above).

In the Minkowski picture (inertial observers with no gravity), not only can you slice spacetime horizontally, you can also slice it at an angle. However you slice it, the geometry within each 2D space slice is still Euclidean. That's the "real world" geometry of space that we perceive. Within a space slice you can still measure spatial distance by ds² = dx² + dy². However, by slicing at different angles, you can end up with different distances between two near-vertical lines through 3D spacetime. The 3D Minkowski spacetime has Minkowski geometry ($d\tau^2 = dt^2 - dx^2 - dy^2$). Each 2D space slice has Euclidean geometry ($ds^2 = dx^2 + dy^2$).

When you bring in non-inertial observers (e.g. Rindler), you are now slicing with non-parallel slices. The planes of simultaneity are no longer a constant distance apart. So as you move near-vertically through the slices, the rate at which you cross them varies from place to place. That's time dilation.

An inertial object follows a straight, near-vertical line upward through spacetime. Measured using parallel space slices, the position within each slice moves in a straight line at constant velocity. Measured using non-parallel slices, the position within each slice might curve or change speed. But this isn't due to the "curvature of spacetime" (which in the absence of gravity isn't curved and does not change when you slice it differently). It's due to non-parallel slicing.

Picturing the track observer central to a sphere of brief fireworks , a quick flash of small points which he would perceive as a single event. Then imagining ,from the track point of view, the same occurance happening on the train. Where the points would start at the rear and proceed forward to the front while the observer was moving.
It seemed sure that the geometry was ellipsoid ,so I concluded that a sphere in one frame was extended through time to become an ellipsoid in another frame.?
I also assume that the observer is located at one locus at the beginning and at the other locus when perceiving the flash but have never sat down to really work it out.
Wouldn't these be a " 3D surfaces in 4D space time that are a constant spacetime interval (=the "pseudo-distance" of spacetime) from an event" ?
So I am trying to equate this with the hyperbola. And figure out if the hyperbola relates to the geometry of the real world or to Minkowski slices of that world , where light spheres are light cones etc.?

In your fireworks scenario, the flashes occur simultaneously in a circle in one frame (sticking with 2D space geometry). They occur non-simultaneously in an ellipse in another frame. They occur within one slice through the hyperboloid. For one observer they are all in one of his own slices in a circle. The other observer has to project that circle into one of this own slices at an angle to the first, and the projection converts a circle to an ellipse.

If we modify your experiment and consider lots of fireworks all launched from a single point simultaneously, at all possible constant velocities, i.e. in all directions at all speeds. Each firework explodes exactly 5 seconds after launched as measured by its own clock. All the explosion events occur on a spacetime hyperboloid, because each has a proper time of 5 secs relative to the launch event. However the events don't all occur simultaneously according to an inertial observer, due to the differing speeds and differing time dilations. The firework that is stationary relative to the observer will explode first, followed by an expanding circle of explosions. At any given moment in time, all the explosions that occur at that moment will be in a circle. (Imagine a horizontal plane of simultaneity moving upward through the hyperboloid.) All inertial observers will agree with the description just given, no matter what their speed, though they'll disagree over the order in which individual fireworks explode.

(To avoid misunderstanding, we are talking about where and when fireworks explode as measured in an observer's coordinate system, not about what an observer would see with his or her eyes.)


Note I have responded here to your latest post only. If there are any outstanding issues from previous posts, please bring them to my attention.

 

[Austin0]

Hi DrGreg glad you're back.

=DrGreg;2334112]The lines of simultaneity tell you how an observer compares one clock against another. To compare two clocks you need to read both simultaneously, then a short while later read both simultaneously again. Divide one clock's time difference by the other's to calculate their relative rates.

I hope you can bear with me . I want to get this question of lines of simultaneity totally clear, both for my understanding and also for [hopefully] further communication between us.
So for now can we confine the question to purely inertial frames?
I have attached one of the diagrams with references for this.
It is understood that these points are purely arbitrary . That the lines apply throughout, to any point on the simultaneity line or any point on the x-axis for the rest frame. SImply by projecting orthogonal lines from the x-axis and the t axis to any point on the x' line of simultaneity or vice-versa.

So these four points A , B, C, D all relate to the same pair of spacetime locations
Those being t=12.5 at x=0 and t'=7.5 at x'=0
Taken all together they portray the temporal relationship between the two , at this point. Further projections accurately portray the relationship between the complete frames at this particular point in time ,,if we consider them both to be extended in space with clocks dispersed throughout.

SO point [A ] graphs the colocation event of (t=12.5 ,x=0) and (t'=20.8 , x'=16.67)

graphs the event (t'=7.5 ,x'=0 ) and (t=12.5 ,x=10 )

[C] (t'=7.5,x' =-6) and (t=4.5 ,x=0 )

[D] ( t'=20.8, x'=0) and (t=34.3 , x=27.7)

1) If there are observers throughout the systems both frames would agree on these events and the temporal relationship between the frame's clocks. That lines of simultaneity are a completely valid, objective graphing of clock relationships between frames at specific locations.

2) This relationship is valid even if there are no observers or if the frame is limited in extent
I.e. Even if x'=0 is a single clock moving up its worldline ,the lines of simultaneity still pertain, with the meaning that this is the relationship that would exist if there was a clock at whatever point in the line of simultaneity that was being considered.

3) That although both frames agree on the simultaneity of these colocation events , there is NO agreement regarding simultaneity between [ A and B ] or [ B and C] or [A and C ] or [A and D] Simultaneity is not transitive between frames regarding spatially separated events or temporal relationships.
So you can pick any point on ( x' = 0 )'s worldline at (t'= k) and the line of simultaneity for that point will tell you what time a clock in the other frame at any chosen location would read coincident with a clock at the appropriate x' = j , t'=k.
But that does not tell you anything meaningful about the temporal relationship between x'=0 and that location in the other frame.

4) That the lines of simultaneity also have a definite spatial meaning. Distance and location within the frame.
That the fact that there is a slope is just an artifact of the conventions of Minkowski space , in the real world , they represent, they are spatially congruent.
So in this instance the length in the diagram of C <----> B has a strict geometric interpretation and represents a specific location on the x' axis. It has the same relationship spatially to A,B that the worldline of S' has, temporally, to the worldline of S

So it would be great to get your feedback on these points , correction or agreement.
I have a feeling this is a very crucial part of the picture and want to get it very clear in my head.
Thanks again

 

[DrGreg]

So these four points A , B, C, D all relate to the same pair of spacetime locations
Those being t=12.5 at x=0 and t'=7.5 at x'=0
Taken all together they portray the temporal relationship between the two , at this point. Further projections accurately portray the relationship between the complete frames at this particular point in time ,,if we consider them both to be extended in space with clocks dispersed throughout.

SO point [A ] graphs the colocation event of (t=12.5 ,x=0) and (t'=20.8 , x'=16.67)

graphs the event (t'=7.5 ,x'=0 ) and (t=12.5 ,x=10 )

[C] (t'=7.5,x' =-6) and (t=4.5 ,x=0 )

[D] ( t'=20.8, x'=0) and (t=34.3 , x=27.7)

In terms of language, I wouldn't speak of a "colocation event". A, B, C and D are events in spacetime that exist independent of any observer. Each observer can assign coordinates to an event. Thus the "unprimed observer" can describe event A as (t=12.5, x=0), and the "primed observer" can describe event A as (t'=20.83, x'=16.67).

1) If there are observers throughout the systems both frames would agree on these events and the temporal relationship between the frame's clocks. That lines of simultaneity are a completely valid, objective graphing of clock relationships between frames at specific locations.

Well, each observer would measure the events in their own coordinate system, but, assuming they understand relativity, they could calculate what the coordinates would be in the other coordinate system.

2) This relationship is valid even if there are no observers or if the frame is limited in extent
I.e. Even if x'=0 is a single clock moving up its worldline ,the lines of simultaneity still pertain, with the meaning that this is the relationship that would exist if there was a clock at whatever point in the line of simultaneity that was being considered.

We speak of a network of rulers and synchronised clocks as a way of visualising how to set up the coordinate system. But the coordinates exist, as a concept, whether the rulers and clocks are actually there or not. In a practical scenario, there may be other methods of determining distance and time coordinates without the physical presence of the rulers or clocks. When analyse a problem theoretically with graphs and equations we can calculate coordinates from theory. In particular, the lines of simultaneity we draw on a spacetime diagram exist as an abstract concept regardless of whether there actually is a network of synchronised clocks.

3) That although both frames agree on the simultaneity of these colocation events , there is NO agreement regarding simultaneity between [ A and B ] or [ B and C] or [A and C ] or [A and D] Simultaneity is not transitive between frames regarding spatially separated events or temporal relationships.

As I said before, don't think of (t=12.5, x=0) and (t'=20.83, x'=16.67) as being two different simultaneous events. They are two different ways of describing the same event. But apart from that quibble, yes, in the unprimed frame, A and B are simultaneous, A and C occur at the same place. In the primed frame, B and C are simultaneous, A and D are simultaneous, and B and D occur at the same place.

So you can pick any point on ( x' = 0 )'s worldline at (t'= k) and the line of simultaneity for that point will tell you what time a clock in the other frame at any chosen location would read coincident with a clock at the appropriate x' = j , t'=k.
But that does not tell you anything meaningful about the temporal relationship between x'=0 and that location in the other frame.

Agreed.

4) That the lines of simultaneity also have a definite spatial meaning. Distance and location within the frame.

Yes, you measure spatial distance along your own frame's lines of simultaneity. (Of course you don't measure the distance as Euclidean diagonal distance across your graph paper.)

That the fact that there is a slope is just an artifact of the conventions of Minkowski space , in the real world , they represent, they are spatially congruent.
So in this instance the length in the diagram of C <----> B has a strict geometric interpretation and represents a specific location on the x' axis. It has the same relationship spatially to A,B that the worldline of S' has, temporally, to the worldline of S

Yes.

You could, if you wanted to, redraw the entire diagram with the t' axis vertical and x' axis horizontal, and therefore the t and x axes both tilted. That would be an equally valid diagram and would be showing exactly the same spacetime "at a different angle" in Minkowski geometry. It would be the equivalent of rotating a Euclidean diagram through an angle.

 

[Austin0]

Hi DrGreg Thank you . You have made me very happy. Not only does it appear that I haven't wandered far off into the brush with my understanding of the basic meaning and function of the graph , but it also appears we may be in agreement regarding the interpretation of the graph.

In terms of language, I wouldn't speak of a "colocation event". A, B, C and D are events in spacetime that exist independent of any observer. Each observer can assign coordinates to an event. 1) Thus the "unprimed observer" can describe event A as (t=12.5, x=0), and the "primed observer" can describe event A as (t'=20.83, x'=16.67).

OK. It is understood that the events exist independant of any observer. The observers were just for illustration and clarity. But I am not sure about 1)
It seems to me that (t=12.5, x=0) is not an event, it is just a spacetime location.
If the event was for instance, a light flash , wouldn't the description be (light flash) at (t=12.5, x=0)
In this case isn't the event [the hypothetical observer at (t=12.5, x=0) looking up and observing the clock at (t'=20.83, x'=16.67) ] ?.
I am not quibbling I just want to learn the correct convention.


Originally Posted by Austin0
1) If there are observers throughout the systems both frames would agree on these events and the temporal relationship between the frame's clocks. That lines of simultaneity are a completely valid, objective graphing of clock relationships between frames at specific locations.

Well, each observer would measure the events in their own coordinate system, but, assuming they understand relativity, they could calculate what the coordinates would be in the other coordinate system.

Understood. Of course, I "calculated" the events for the diagram in question. The purpose of the hypothetical observers, both for illustration and for my own understanding, was that they would not have to know relativity or calculate anything. They would only have to look at the actual clock readings of their own clock and the other frame's clock and look at the ruler markings as a purely empirical [objective] observation.


Originally Posted by Austin0
2) This relationship is valid even if there are no observers or if the frame is limited in extent
I.e. Even if x'=0 is a single clock moving up its worldline ,the lines of simultaneity still pertain, with the meaning that this is the relationship that would exist if there was a clock at whatever point in the line of simultaneity that was being considered.


Originally Posted by Austin0
3) That although both frames agree on the simultaneity of these colocation events , there is NO agreement regarding simultaneity between [ A and B ] or [ B and C] or [A and C ] or [A and D] Simultaneity is not transitive between frames regarding spatially separated events or temporal relationships.

As I said before, don't think of (t=12.5, x=0) and (t'=20.83, x'=16.67) as 2) being two different simultaneous events. They are two different ways of describing the same event. But apart from that quibble, yes, in the unprimed frame, A and B are simultaneous, A and C occur at the same place. In the primed frame, B and C are simultaneous, A and D are simultaneous, and B and D occur at the same place.

2) I was thinking of them as being one simultaneous event. Simultaneous within the only absolute meaning of simultaneous there is ,, I.e. occurring at the same location at one time. That any passing inertial observer [at any velocity] would agree that the colocation of [(t=12.5, x=0),(t'=20.83, x'=16.67)] was a simultaneous occurence. Once again I am not quibbling , so please correct me if I don't have it right.
On the non-transitivity of simultaneity of spatially separated events between frames;
Am I correct in thinking that you agree ?
It seems to me that this is the cause of a whole lot of confusion within this forum and the world at large. The tendency to attribute pre-SR ideas of absolute simultaneity to situations where they don't apply. Eg: the twins paradox. The paradox is not what happens when the twins are re-colocated. Reality precludes a paradox in this case. The real paradox takes place when the space twin keeps on trucking. In this case if you try to define some kind of absolute temporal relationship [which requires an absolute simultaneity] you run right into the "both being older than the other conundrum". And the common resolution that "well both evaluations are true from their own perspective" is not any kind of resolution , nor is it at all logical. I understand the SR version of block time, where every particle in spacetime resides in a unique slice of simultaneous "Now" with complex topography, that itself moves through the pre-existent worldlines. I understand it and can conceptualize it very well. in fact have been considering doing an animated graphic of it , [great subject] but I can neither accept or reject it. It is a metaphysical conception. Based on the assumption of a meta-reality with hyperphysics that is a priori beyond our logic or comprehension. Translogical.
So in all cases there is no meaningful evaluation to be assigned. The age difference is as indeterminable as Schrodingers cat.


Originally Posted by Austin0
4) That the lines of simultaneity also have a definite spatial meaning. Distance and location within the frame.

Yes, you measure spatial distance along your own frame's lines of simultaneity. (Of course you don't measure the distance as Euclidean diagonal distance across your graph paper.)

Understood it must be transformed

You could, if you wanted to, redraw the entire diagram with the t' axis vertical and x' axis horizontal, and therefore the t and x axes both tilted. That would be an equally valid diagram and would be showing exactly the same spacetime "at a different angle" in Minkowski geometry. It would be the equivalent of rotating a Euclidean diagram through an angle.

Isn't this just the standard complementary or mirror image diagram that is often done with two frames??

Well I seem to be talking your ear off here, so thank you so much,, you have really helped

 

[DrGreg]

OK. It is understood that the events exist independant of any observer. The observers were just for illustration and clarity. But I am not sure about 1)
It seems to me that (t=12.5, x=0) is not an event, it is just a spacetime location.
If the event was for instance, a light flash , wouldn't the description be (light flash) at (t=12.5, x=0)
In this case isn't the event [the hypothetical observer at (t=12.5, x=0) looking up and observing the clock at (t'=20.83, x'=16.67) ] ?.
I am not quibbling I just want to learn the correct convention.

In the technical jargon of spacetime an "event" is the name we give to a zero-dimensional "point" in 4D spacetime. We avoid the use of the word "point" because of possible confusion with a point in 3D space, which becomes a 1D line ("worldline") in spacetime. So the flash is an event, one observer says the coordinates of the flash event are (12.5, 0), another observer says the coordinates of that same flash event are (20.83, 16.67).

However, in practice, people often use the word "event" more loosely than that, so don't worry about it. For example we may speak of the event of Alice's clock showing 3pm and the event of Bob's clock showing 4pm. If both of these happen as Alice & Bob pass each other, we could say "both events occur at the same place and time".

The purpose of the hypothetical observers, both for illustration and for my own understanding, was that they would not have to know relativity or calculate anything. They would only have to look at the actual clock readings of their own clock and the other frame's clock and look at the ruler markings as a purely empirical [objective] observation.

Agreed.

2) I was thinking of them as being one simultaneous event. Simultaneous within the only absolute meaning of simultaneous there is ,, I.e. occurring at the same location at one time. That any passing inertial observer [at any velocity] would agree that the colocation of [(t=12.5, x=0),(t'=20.83, x'=16.67)] was a simultaneous occurence. Once again I am not quibbling , so please correct me if I don't have it right.

Agreed.

On the non-transitivity of simultaneity of spatially separated events between frames;
Am I correct in thinking that you agree ?
It seems to me that this is the cause of a whole lot of confusion within this forum and the world at large. The tendency to attribute pre-SR ideas of absolute simultaneity to situations where they don't apply. Eg: the twins paradox. The paradox is not what happens when the twins are re-colocated. Reality precludes a paradox in this case. The real paradox takes place when the space twin keeps on trucking. In this case if you try to define some kind of absolute temporal relationship [which requires an absolute simultaneity] you run right into the "both being older than the other conundrum". And the common resolution that "well both evaluations are true from their own perspective" is not any kind of resolution , nor is it at all logical. I understand the SR version of block time, where every particle in spacetime resides in a unique slice of simultaneous "Now" with complex topography, that itself moves through the pre-existent worldlines. I understand it and can conceptualize it very well. in fact have been considering doing an animated graphic of it , [great subject] but I can neither accept or reject it. It is a metaphysical conception. Based on the assumption of a meta-reality with hyperphysics that is a priori beyond our logic or comprehension. Translogical.
So in all cases there is no meaningful evaluation to be assigned. The age difference is as indeterminable as Schrodingers cat.

Pretty much. We have conventions to say what the age difference is relative to any frame, but the answers are all different and there's no reason to choose anyone of them as the best answer.

I'm not sure I'd agree it's "beyond our logic or comprehension". If we can write down equations that correctly predict the outcome of any experiment, then, arguably, we do understand what is happening. But there comes a point when we can't give any further reasons why the Universe behaves the way it does. We just have to accept that's the way it is.

Also I'm not quite sure of your use of the word "transitivity". My understanding of that word is the mathematical definition. In this context we could ask, if A is simultaneous with B, and B is simultaneous with C, is A simultaneous with C? The answer to that (for all possible A, B and Cs) determines whether "simultaneous" is a transitive relation or not.

Isn't this just the standard complementary or mirror image diagram that is often done with two frames??

Yes. (Of course, the axes are mirrored, but if there are other things on the diagram too, the whole diagram might not be a mirror image.)

 

[Austin0]

I'm not sure I'd agree it's "beyond our logic or comprehension". If we can write down equations that correctly predict the outcome of any experiment, then, arguably, we do understand what is happening. But there comes a point when we can't give any further reasons why the Universe behaves the way it does. We just have to accept that's the way it is.

It appears you may have thought I was referring to SR when I used those terms.
I was not at all. I was talking about block time as conceived by many within SR.
When I said beyond our logic I meant in the sense that you cannot logically verify or support concepts like block time or Wheelers worlds . You cannot logically derive a physics that would make them actual possibilities.Or comprehend them beyond the most simplistic verbal descriptions [equivalent to paper galaxies on an expanding balloon].
At the same time you cannot logically refute or reject them on any basis of reason or physics that applies to our reality. It would be silly to even try.
Dont misunderstand me. When I use the term Metaphysical , I don't mean that in any negative sense. I have plenty of ideas and feelings regarding this realm. I would hope that any final theory of physics would somehow bring it all together, pointing to some higher reality , have resonance with the human spirit as well as the intellect.
But the point I was trying to convey is that even if SR block time is a reality , it is a many worlds concept. And any entity at a spatial remove is effectively in another universe. It does not provide any meaningful information or helpful concepts. It does not resolve any paradoxes ,it IS a paradox.
So if the Lorentz dilation calculation tells us that Fred is 100 while Bill is 13 and also tells us that Fred is 13 while Bill is 100 , what does this mean? To give any validity to either one, is to attempt to apply an absolute simultaneity. To assume that there is a definite, quantifiable , instantaneous relationship between them over a large distance.
No , actually two ,different, mutually exclusive, definite , quantifiable instantaneous temporal relationships. Yet SR has made it clear that we cannot assume any real simultaneity even at much closer distances. So I just don't know?

Also I'm not quite sure of your use of the word "transitivity". My understanding of that word is the mathematical definition. In this context we could ask, if A is simultaneous with B, and B is simultaneous with C, is A simultaneous with C? The answer to that (for all possible A, B and Cs) determines whether "simultaneous" is a transitive relation or not.

This is the definition I was using but I see that I may have been ,at best, using it obscurely, if not actually incorrectly.

SO point [A ] graphs the colocation event of (t=12.5 ,x=0) and (t'=20.8 , x'=16.67)

Blue IS simultaneous with Red


graphs the event (t'=7.5 ,x'=0 ) and (t=12.5 ,x=10 )

Green IS simultaneous with Red

But: Green IS NOT simultaneous with Blue

And:

(t=12.5 ,x=0) and (t'=20.8 , x'=16.67) IS NOT simultaneous with

(t'=7.5 ,x'=0 ) and (t=12.5 ,x=10 )

Therefore it would appear that :
(t=12.5 ,x=0) CAN NOT be simultaneous with
(t=12.5 ,x=10 )

Except withiin a limited ,conditional definition when applied to the measuring of physical phenomena within the frame. In this context, it self-evidently works perfectly ,without problem, but also without the neccessity of any assumption or implication of actual or absolute simultaneity.

I have studied the hyperbola and lightcone diagram. I can't really conceive of the shape of the hyperbola if it is fully realized in 3 D with the lightcone being a light sphere.
It seems like it would not be a bounded shape but would be some kind of complex gradient or something. But I will keep trying.
Thanks



[