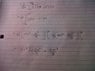- #1
azserendipity
- 10
- 0
Homework Statement
Please take into account I'm not very good at maths so I would just like to make sure that what I am doing so far is correct
Obtain the Fourier transform for:
f(x) = x(2∏-x) 0<x<2∏ f(x)=f(x+2∏)
Homework Equations
f(x) = 1/2 a0 + Ʃ {an cosnx + bn sinnx} = ao/2 + a1cosx +a2cos2x + b1sinx+b2sin2x +...
The Attempt at a Solution
an = 1/x ∫x(2∏-x)cos(nωt) dt
I've attached the rest of my working out below: