Fourier series of this scale and shift of triangle wave

[zenterix]

Homework Statement

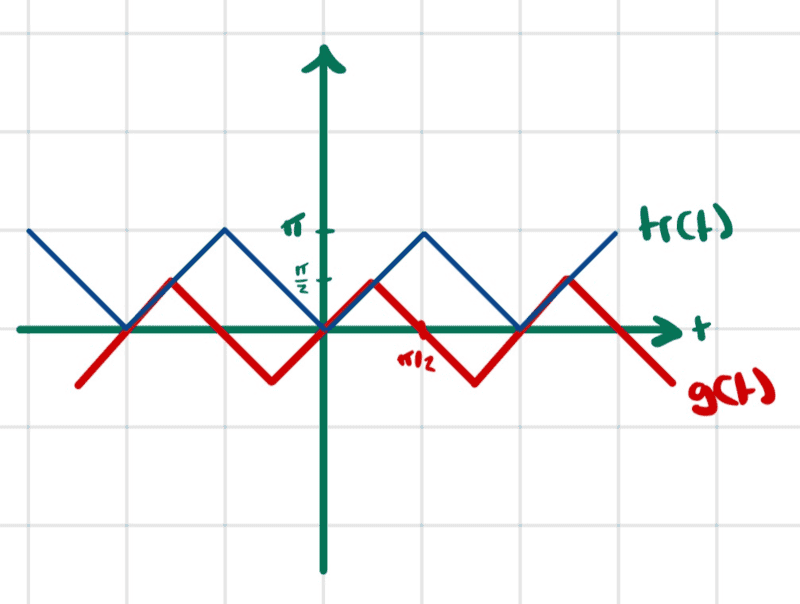
Consider the periodic function of period $2\pi$

Relevant Equations

$$g(t)=\begin{cases} t\ \ \ \ \ -\frac{\pi}{2}<t<\frac{\pi}{2} \\ \pi-t\ \ \ \ \ \frac{\pi}{2}<t<\frac{3\pi}{2} \end{cases}\tag{1}$$

This function seems to be $tr\left (t+\frac{\pi}{2}\right )-\frac{\pi}{2}$ where $tr(t)$ is the triangle wave function.

$$tr(t)=|t|\ \ \ \ \ -\frac{\pi}{2}<t<\frac{\pi}{2}\tag{2}$$

$tr$ has Fourier series

$$tr(t)=\frac{\pi}{2}-\frac{4}{\pi}\sum\limits_{n=1}^\infty \frac{\cos{(nt)}}{n^2}\tag{2a}$$

Thus

$$g(t)=tr\left (t+\frac{\pi}{2}\right )-\frac{\pi}{2}\tag{3}$$

$$-\frac{4}{\pi}\sum\limits_{n=1}^\infty \frac{\cos{\left (n\left (t+\frac{\pi}{2}\right ) \right )}}{n^2}\tag{4}$$

Now

$$\cos{\left ( nt +n\frac{\pi}{2} \right )}=\cos{(nt)}\cos{\left (\frac{n\pi}{2}\right )}-\sin{(nt)}\sin{\left (\frac{n\pi}{2}\right )}\tag{5}$$

$$\sum\limits_{n=1}^\infty \cos{\left ( nt +n\frac{\pi}{2} \right )} = (-\sin{t})+(-\cos{2t})+(\sin{3t})+(\cos{4t})+(-\sin{5t})+(-\cos{6t})+\ldots\tag{6}$$

$$=\sum\limits_{k=0}^\infty (-1)^{k+1}\sin{(2k+1)t}+\sum\limits_{k=1}^\infty (-1)^k \cos{(2kt)}\tag{7}$$

If we sub this expression into (4) then

$$g(t)=-\frac{4}{\pi}\left ( \sum\limits_{k=0}^\infty (-1)^{k+1}\frac{\sin{(2k+1)t}}{(2k+1)^2}+\sum\limits_{k=1}^\infty (-1)^k \frac{\cos{(2kt)}}{(2k)^2} \right )\tag{8}$$

If the calculations are correct so far, my question is why this Fourier series has both cosine and sine terms when $g$ is odd.

 

[zenterix]

I think I need to take a break from studying today.

The answer to my question is a silly mistake.

Equation (2a) is incorrect. The summation is only over odd $n$

$$tr(t)=\frac{\pi}{2}-\frac{4}{\pi}\sum\limits_{n\ \text{odd}} \frac{\cos{(nt)}}{n^2}\tag{2a}$$

Thus, equation (4) is also only over odd $n$

$$-\frac{4}{\pi}\sum\limits_{n\ \text{odd}}^\infty \frac{\cos{\left (n\left (t+\frac{\pi}{2}\right ) \right )}}{n^2}\tag{4}$$

and in (5), since $n$ is odd then the first term on the rhs is zero

$$\cos{\left ( nt +n\frac{\pi}{2} \right )}=-\sin{(nt)}\sin{\left (\frac{n\pi}{2}\right )}\tag{5}$$

$$=\sum\limits_{k=0}^\infty (-1)^{k+1} \sin{((2k+1)t)}\tag{7}$$

Hence

$$g(t)=-\frac{4}{\pi}\left ( \sum\limits_{k=0}^\infty (-1)^{k+1}\frac{\sin{(2k+1)t}}{(2k+1)^2} \right )\tag{8}$$