Fourier series, periodic function for a string free at each end

[Redwaves]

Homework Statement

A string of length = L with a mass = M fixed to a ring at each end, but the ring is free to move. The rings are massless and we neglected the gravity.
At t = 0 the rings are at y = 0 and the string has the same form that $y(x,0) = Asin(\frac{2 \pi x}{L})$
We release the rings at t = 0

Find $f(x)$ from initials and boundaries conditions

Relevant Equations

$f(x) = \frac{A_0}{2} + \sum A_n cos(\frac{n2 \pi x}{P} ) + \sum B_n sin(\frac{2n \pi x}{P}) )$

From the statement above, since the ring is massless, there's no force acting vertically on the rings. Thus, the slope is null.

$\frac{\partial y(0,0)}{\partial x} = \frac{\partial y(L,0)}{\partial x} = 0$

$\frac{\partial y(0,0)}{\partial x} = A\frac{2 \pi}{L}cos(\frac{2 \pi 0}{L}) = \frac{\partial y(L,0)}{\partial x} = A\frac{2 \pi}{L}cos(\frac{2 \pi L}{L}) = 0$

Here I have a problem, since $A\frac{2 \pi}{L}cos(\frac{2 \pi 0}{L}) = 0$ only If A = 0

Thus, $f(x) = \frac{A_0}{2} + \sum 0 cos(\frac{n2 \pi x}{P} ) + \sum B_n sin(\frac{2n \pi x}{P}) ) = f(x) = \frac{A_0}{2} + \sum B_n sin(\frac{2n \pi x}{P}) )$

Since cos is a symmetric function, from the graph I made, the period should be 2L, since at every "0" and "L" the string must be symmetric at each side.

Now, with the initials conditions (position and velocity) .
I don't fully understand the periodic function. Is the second sum in the function about the initials conditions?

Here's what I got.

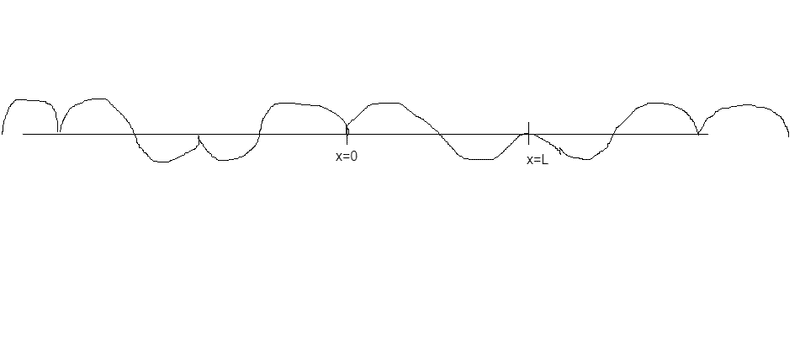
Edit: Can I say that the periodic function is
$f(x) = \frac{A_0}{2} + \sum_1^{\infty} A_n cos(\frac{n2 \pi x}{2L} ) + \sum_1^{\infty} B_n sin(\frac{2n \pi x}{2L})$

 

[TSny]

The set of functions $\cos(\frac {n 2\pi x}{P})$ for $n = 1, 2, 3, ...$ with $P = 2L$ satisfy the boundary conditions of zero slope at $x = 0$ and $x = L$. So, these would be the Fourier basis functions for this problem. Since $P = 2L$, you may write these as $\cos(\frac {n \pi x}{L})$.

The initial shape of the string is $A\sin(\frac {n\pi x}{L})$. This function has nonzero slope at the endpoints. Thus, if you release the string with this initial shape, the tension in the string would cause the massless rings to have infinite acceleration! So, it's not really an acceptable shape. However, you can imagine that the initial shape of the string approximates the shape $A\sin(\frac {n\pi x}{L})$ to a high degree of approximation (except that very close to the endpoints the string bends to have zero slope).

So, the question is whether or not you can approximate $A\sin(\frac {n\pi x}{L})$ (which has nonzero slope at the ends) as a Fourier series using the functions $\cos(\frac {n\pi x}{L})$ (which have zero slope at the ends). The answer is yes.

See if you can determine the coefficients $A_n$ so that $\sum A_n\cos(\frac {n\pi x}{L}) =A\sin(\frac {n\pi x}{L})$.

 

[Redwaves]

Using the formula
$A_n = \frac{2}{p}\int_0^{P} f(x,0) cos(\frac{n \pi x }{L}) dx$
$A_n = \frac{1}{L}\int_0^{2L} d sin(\frac{2 \pi x}{L}) cos(\frac{n \pi x }{L}) dx$

$A_n = \frac{d}{L}\int_0^{2L} \frac{1}{2}[ sin(\frac{(2+n)\pi x}{L}) - sin(\frac{(-2+n)\pi x}{L})] dx$

I get 0 for $A_n$ which isn't correct.

I think I have to split the integral into 2 parts. Because $sin(\frac{2 \pi x}{L})$ isn't symmetric.

 

[TSny]

$A_n = \frac{2}{p}\int_0^{P} f(x,0) cos(\frac{n \pi x }{L}) dx$

I think this should be $A_n = \frac{2}{L}\int_0^L f(x,0) \cos(\frac{n \pi x}{L}) dx$

 

[TSny]

The formula $A_n = \frac{2}{P}\int_0^P f(x,0) \cos(\frac{n \pi x}{L}) dx$ will give the same result as $A_n = \frac{2}{L}\int_0^L f(x,0) \cos(\frac{n \pi x}{L}) dx$ if you use the "extended" function $f(x,0)$ that you graphed in your first post.

Note that for $0<x<L$, $f(x,0) =A\sin(\frac{2 \pi x}{L})$ but for $L < x < 2L$, $f(x,0) = -A\sin(\frac{2 \pi x}{L})$.

So, $\frac{2}{P}\int_0^P f(x,0) \cos(\frac{n \pi x}{L}) dx =$

$\frac{2}{2L}\int_0^{2L} f(x,0) \cos(\frac{n \pi x}{L}) dx =$

$\frac{1}{L}\left[ \int_0^L A\sin(\frac{2 \pi x}{L}) \cos(\frac{n \pi x}{L}) dx + \int_L^{2L}-A\sin(\frac{2 \pi x}{L}) \cos(\frac{n \pi x}{L}) dx \right]$

The second integral yields the same result as the first integral. So, the overall result can be written simply as

$\frac{2}{L}\int_0^L A\sin(\frac{2 \pi x}{L}) \cos(\frac{n \pi x}{L}) dx = \frac{2}{L}\int_0^L y(x,0) \cos(\frac{n \pi x}{L}) dx$

 

[Redwaves]

So, n must be odd, because if n is even $A_n$ = 0, right?

 

[TSny]

So, n must be odd, because if n is even $A_n$ = 0, right?

Yes, that's right.

 

[Redwaves]

Thanks! it's so much clearer.

 

[Bobbo]

Thanks! it's so much clearer.

which book is that exercise from?