- #1
PainterGuy
- 940
- 70
- TL;DR Summary
- Trying to understand the requirements for a function to be represented by a Fourier series
Hi,
A function which could be represented using Fourier series should be periodic and bounded. I'd say that the function should also integrate to zero over its period ignoring the DC component.
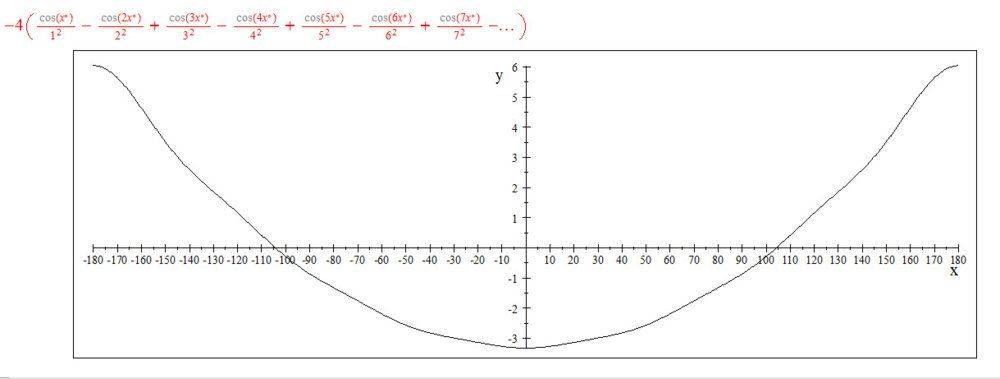
For many functions area from -π to 0 cancels out the area from 0 to π. For example, Fourier series representation #1 below approximates such a function.
For some functions area from -π to -π/2 cancels out area from -π/2 to 0, and then area from 0 to π/2 gets canceled by the area from π/2 to π. For example, Fourier series representation #2 below approximates such a function.
I'm not sure if the function needs to integrate to zero following these two patterns, or it should just amount to zero without actually following any pattern of area cancellation. Could you please let me know if I have it right?
Could you represent a function something like this using Fourier series? I'm just trying to get general concept about Fourier series right. Thank you for your help.
Fourier series representations #1

Fourier series representations #2
A function which could be represented using Fourier series should be periodic and bounded. I'd say that the function should also integrate to zero over its period ignoring the DC component.
For many functions area from -π to 0 cancels out the area from 0 to π. For example, Fourier series representation #1 below approximates such a function.
For some functions area from -π to -π/2 cancels out area from -π/2 to 0, and then area from 0 to π/2 gets canceled by the area from π/2 to π. For example, Fourier series representation #2 below approximates such a function.
I'm not sure if the function needs to integrate to zero following these two patterns, or it should just amount to zero without actually following any pattern of area cancellation. Could you please let me know if I have it right?
Could you represent a function something like this using Fourier series? I'm just trying to get general concept about Fourier series right. Thank you for your help.
Fourier series representations #1
Fourier series representations #2


