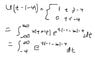- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Fourier transform (integration)
- Thread starter gomes.
- Start date
In summary, The conversation discusses the definition of the Fourier transform and how to solve a problem involving it. The first part involves using the step function to replace the lower limit of the integral, while the second part involves integrating the function u(t+4)e^(t(-1-iw)-4). The unit step function is also mentioned as a helpful resource. The conversation ends with confirmation that the integrals are correct and a suggestion to use the substitution t'=t+4 to evaluate the integral.
Physics news on Phys.org
- #2
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,098
- 2,745
What's the definition of the Fourier transform? The problem is asking you to find the Fourier transform of that function using it.
- #3
- #4
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,098
- 2,745
The step function makes the integrand equal to 0 when t+4<0, so that let's you replace the lower limit of the integral with -4.
- #5
gomes.
- 58
- 0
thanks, but how would i integrate u(t+4)e^[t(-1-iw)-4]?
How do i deal with the u(t+4)?
How do i deal with the u(t+4)?
- #6
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,098
- 2,745
What is u(t+4) equal to for t>-4?
- #7
gomes.
- 58
- 0
sorry I am really stuck, u(t)?
- #8
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,098
- 2,745
The unit step function must surely be discussed in your notes or textbook.
http://www.efunda.com/math/unit_delta/unit_delta.cfm
http://www.efunda.com/math/unit_delta/unit_delta.cfm
- #9
- #10
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,098
- 2,745
Well, the first line definitely doesn't equal the second line.
The integrals look okay.
The integrals look okay.
- #11
gomes.
- 58
- 0
sorry, I am really really stuck. What should the next line be, after the first line? Could someone possibly show me how to proceed from the 1st line?
- #12
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,098
- 2,745
Perhaps you misunderstood. I meant:
[tex]u(t) \ne \int_{-\infty}^\infty u(t+4) e^{t(-1-i\omega)-4}\,dt[/tex]
The integral in the second line is fine to calculate the Fourier transform you're looking for, but it's definitely not equal to u(t) as you wrote.
Try the substitution t'=t+4 to evaluate the integral.
[tex]u(t) \ne \int_{-\infty}^\infty u(t+4) e^{t(-1-i\omega)-4}\,dt[/tex]
The integral in the second line is fine to calculate the Fourier transform you're looking for, but it's definitely not equal to u(t) as you wrote.
Try the substitution t'=t+4 to evaluate the integral.
- #13
gomes.
- 58
- 0
thanks! got it now
FAQ: Fourier transform (integration)
What is a Fourier transform?
A Fourier transform is a mathematical operation that decomposes a function into its frequency components. It takes a function in the time or spatial domain and converts it into a function in the frequency domain, showing the amplitude and phase of each frequency component.
How is a Fourier transform calculated?
The Fourier transform is calculated by integrating the function over its entire domain using a specific formula. This formula involves complex numbers and involves breaking down the function into its sine and cosine components.
3. What are the applications of a Fourier transform?
Fourier transforms have a wide range of applications in various fields such as signal processing, image processing, and data compression. They are also used in solving differential equations and in analyzing the frequency content of a signal.
4. What is the difference between a Fourier transform and a Fourier series?
A Fourier transform is used for continuous functions with an infinite domain, while a Fourier series is used for periodic functions with a finite domain. A Fourier transform gives a continuous spectrum of frequencies, while a Fourier series gives a discrete spectrum of frequencies.
5. Are there any limitations to using Fourier transforms?
Fourier transforms assume that the function is periodic and has a finite energy. They also assume that the function is well-behaved and has no sudden changes or discontinuities. These limitations may affect the accuracy of the results in some cases.
Similar threads
- Replies
- 5
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 1
- Views
- 214
- Replies
- 6
- Views
- 987
- Replies
- 23
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 6
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 1K
Share: