Graduate Fourier Transform of a piecewise function

[Houeto]

Here is the Problem Statement : Find Fourier Transform of the piecewise function

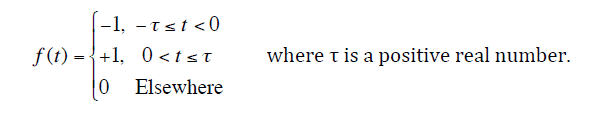
Can someone sheds some lights on how to start solving this?

Thanks

 

[absalonsen]

The Fourier transform of your function f(t) is given as:

$$ F\left[f(t)\right] = \int_{-\infty}^{\infty} dt e^{i\omega t}f(t) = \int_{-\tau}^{0} -e^{i\omega t}dt + \int_{0}^{\tau} e^{i\omega t}dt $$

In the last step, I made use of the fact that f(t) is 0 elsewhere. As a final step, one can perform a simple integration to solve for the Fourier transform of f(t).

 

[Houeto]

Thanks Absalonsen! Is it e^(iwt) or e^(-iwt)?Let me know.

 

[absalonsen]

Thanks Absalonsen! Is it e^(iwt) or e^(-iwt)?Let me know.

np. It is usually a convention to determine the sign of the exponential in Fourier transform. In physics, forward Fourier transform from time to frequency space is carried out by $e^{-iwt}$, while forward Fourier transform from real space to momentum space contains $e^{ikx}$.

Great work, piecewise functions are not easy to calculate!