durandal
- 5
- 2
- Homework Statement
- Find the Fourier transform of sin(4t-4)
- Relevant Equations
- Regular Fourier transforms
This is my attempt at a solution. I have used Eulers formula to rewrite the sine function and then used the Fourier transform of complex exponentials. My solution is not correct and I don't understand if I have approached this problem correctly. Please help.
$$ \mathcal{F}\{\sin (4t-4) \} = \frac{1}{2j} \mathcal{F} \{ e^{j(4t-4)} - e^{-j(4t-4)} \} $$
$$ \frac{1}{2j}(e^{-4j} \mathcal{F}\{ e^{4jt}\} - e^{4j} \mathcal{F}\{ e^{-4jt} \}) = \frac{1}{2j}(e^{-4j} 2 \pi \delta(\omega - 4)-e^{4j} 2 \pi \delta(\omega + 4))$$
$$ \mathcal{F(\omega)} = \frac{\pi}{j}(e^{-4j} \delta(\omega - 4) - e^{4j}\delta(\omega + 4)) $$
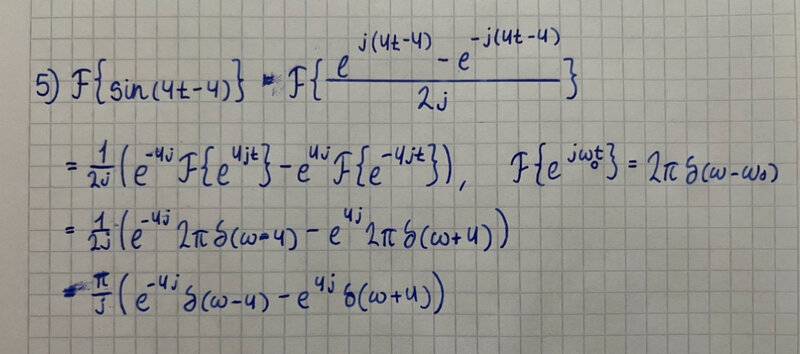
$$ \mathcal{F}\{\sin (4t-4) \} = \frac{1}{2j} \mathcal{F} \{ e^{j(4t-4)} - e^{-j(4t-4)} \} $$
$$ \frac{1}{2j}(e^{-4j} \mathcal{F}\{ e^{4jt}\} - e^{4j} \mathcal{F}\{ e^{-4jt} \}) = \frac{1}{2j}(e^{-4j} 2 \pi \delta(\omega - 4)-e^{4j} 2 \pi \delta(\omega + 4))$$
$$ \mathcal{F(\omega)} = \frac{\pi}{j}(e^{-4j} \delta(\omega - 4) - e^{4j}\delta(\omega + 4)) $$
Last edited by a moderator:
