- #1
nao113
- 68
- 13
- Homework Statement
- Calculate the Fourier transform of rectangular pulse given below. (Height, A; width, 2a)
. I tried to calculate that but I am not sure whether it s correct or not. Do I need to put A there or just omit it so it will just be e^-jwt? thank you
- Relevant Equations
- available in the question
Here is the question:
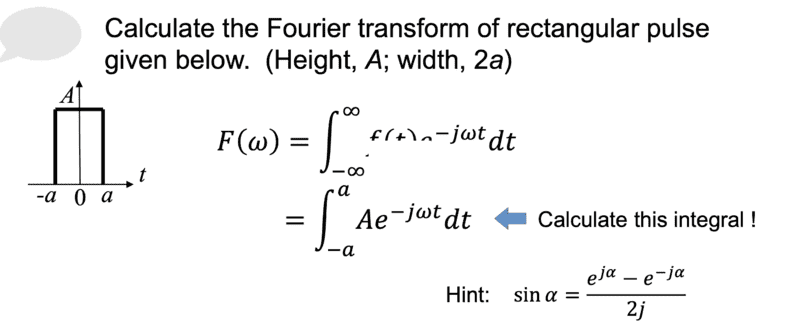
Here is my answer
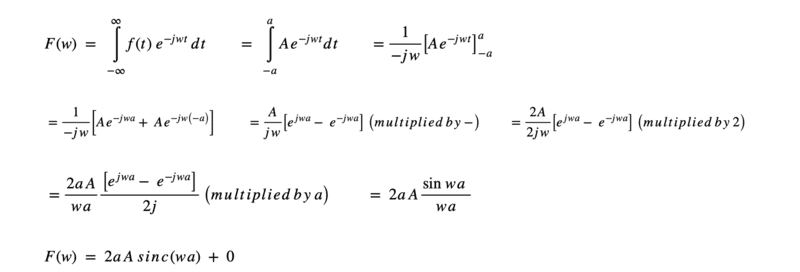
Here is my answer
Last edited:


