- #1
arcTomato
- 105
- 27
- Homework Statement
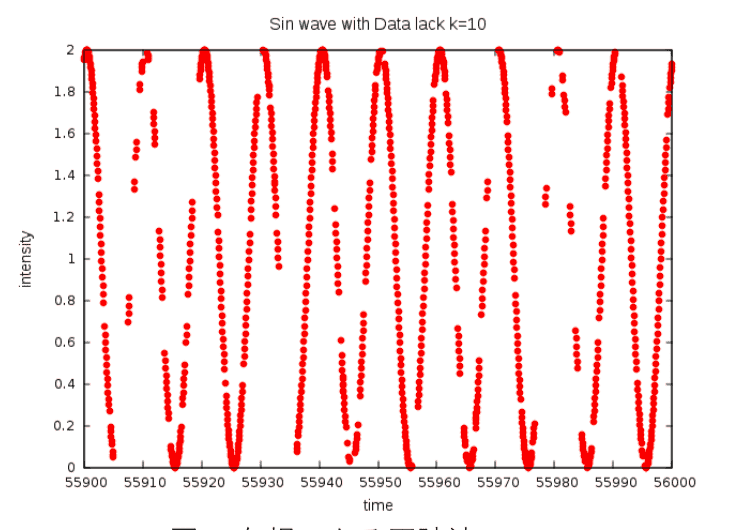
- I would like to know the equation of Fourier transform when the data has lack.
- Relevant Equations
- Fourier transform
I would like to know the equation of Fourier transform when the data has lack. like this sine wave.