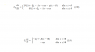Itosu
- 19
- 0
Hello!
I am trying to solve two differential, non-linear equations in C# using fourth-order Runge-Kutha method.
I implemented them in C#:
However the results are not that that should be (in comparison to Simulink model).
Do you have any ideas?
Thank you in advance!
I am trying to solve two differential, non-linear equations in C# using fourth-order Runge-Kutha method.
I implemented them in C#:
Code:
private const int ALFA = 7600;
private const int MU = 7200;
private int BETA = 1430;//int.Parse(HttpContext.Current.Session["BETA"].ToString());
private const int LAMBDA = 2470;
private int V = 139000;//int.Parse(HttpContext.Current.Session["V"].ToString());
private const double FI = 0.51;
private const double TETA = 2.5;
private const int QL = 8400;
private const double H = 0.01;
public double x = 0.81;
public double y = 0.055;
// ;
public ArrayList yList;
public ArrayList xList;
public void Start()
{
xList = new ArrayList();
yList = new ArrayList();
double t = 0;
// xList.
// y = Y0;
for (double krok = 0; krok <= 500; krok++)
{
t = krok / 100;
xList.Add(x);
yList.Add(y);
x = rungeDX(x, t);
y = rungeDY(y, t);
//x = X0 + (i * H);
//y = runge(x, y);
}
}
public double doplyw(double t)
{
if (t >= 0.5 && t < 0.75)
return 100000;
else return 0;
}
private double dx(double x, double y, double t)
{
double result;
if (x > TETA)
result = (doplyw(t) + QL - LAMBDA * x - V * x * y - MU * (x - TETA)) / 15000;
else
result = (doplyw(t) + QL - LAMBDA * x - V * x * y) / 15000;
return result;
}
private double dy(double x, double y)
{
double result;
if (x > FI)
result = (-ALFA * y + BETA * (x - FI)) / 15000;
else
result = (-ALFA * y) / 15000;
return result;
}
double rungeDX(double x, double t)
{
double K1 = dx(this.x, y, t);
double K2 = dx((this.x + 0.5 * H), (y + 0.5 * K1), t);
double K3 = dx((this.x + 0.5 * H), (y + 0.5 * K2), t);
double K4 = dx((this.x + H), (y + K3), t);
double rest = (K1 + 2 * K2 + 2 * K3 + K4) * H;
double runge = this.x + rest;
return runge;
}
double rungeDY(double x, double t)
{
double K1 = dy(x, y);
double K2 = dy((x + 1 / 2 * H), (y + 1 / 2 * K1));
double K3 = dy((x + 1 / 2 * H), (y + 1 / 2 * K2));
double K4 = dy((x + H), (y + K3));
double rest = (K1 + 2 * K2 + 2 * K3 + K4) * H;
double runge = y + rest;
return runge;
}
}However the results are not that that should be (in comparison to Simulink model).
Do you have any ideas?
Thank you in advance!