Gerasimov
- 2
- 0
Greetings, humans! (Tongueout) I'm from Ukraine. My English is very bad. So I will use a Google Translate.
In 2002, I came up with an interesting piece. I was only 14 years old. I was thinking about fractals and chaos theory, and did not want to learn. Did not want to learn, and were forced to walk to school. I came up with a way to kill time on the boring lessons in history, geography, and other humanities. I'll try to explain in detail. All we need - a piece of paper into a cell and an ordinary pencil. If a piece of paper is not available and also no pencil - an online version of JavaScript: New kind of fractals - Fractals in relatively prime integers (coprime integers).
The algorithm is simple to indecency. Actually these things look like this:
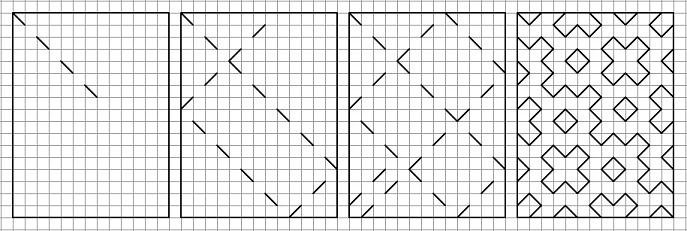
Select the rectangle and let in the corner of the "quantum beam" (as I called it in 2002) The beam reflected from the walls and is lost at the other corner.
If certain conditions were met - it turns fractal pattern.
If the conditions are not met (for example the obvious - the rectangle are equal) - pattern is not obtained. Of the less obvious example - the same pattern as it is impossible, if the size of the parties have a common divisor. In fact, the patterns are obtained only if the dimensions of both sides - are relatively prime (have no common divisor).
Сlickable:

In the picture all the numbers from 1 to 30.
And now a little about Fibonacci and fractals. (Crying)
Patterns represent a fractal.
What determines the pattern?
That suggests to us - what if you try to Fibonacci numbers? "Пацан сказал - пацан сделал" (do not know how to translate it to English :).Painted the largest enclosed area.
233х144:



987х610 (pressed 5 times):
 233х144 и 987х610 - identical :)
233х144 и 987х610 - identical :)
As you can see, fractal repeats part of the overall fractal
Fractals, as they are.
Site: New kind of fractals - Fractals in relatively prime integers (coprime integers)
P.S.
And a little bit schizophrenic 11-year-old:
Perhaps the chaos - it is also a fractal?
In 2002, I came up with an interesting piece. I was only 14 years old. I was thinking about fractals and chaos theory, and did not want to learn. Did not want to learn, and were forced to walk to school. I came up with a way to kill time on the boring lessons in history, geography, and other humanities. I'll try to explain in detail. All we need - a piece of paper into a cell and an ordinary pencil. If a piece of paper is not available and also no pencil - an online version of JavaScript: New kind of fractals - Fractals in relatively prime integers (coprime integers).
The algorithm is simple to indecency. Actually these things look like this:

Select the rectangle and let in the corner of the "quantum beam" (as I called it in 2002) The beam reflected from the walls and is lost at the other corner.
If certain conditions were met - it turns fractal pattern.
If the conditions are not met (for example the obvious - the rectangle are equal) - pattern is not obtained. Of the less obvious example - the same pattern as it is impossible, if the size of the parties have a common divisor. In fact, the patterns are obtained only if the dimensions of both sides - are relatively prime (have no common divisor).
Сlickable:

In the picture all the numbers from 1 to 30.
And now a little about Fibonacci and fractals. (Crying)
Patterns represent a fractal.
What determines the pattern?
So you need to make a difference, too, was a prime number (the largest), its difference with the numbers, too, was simple and small, and so on, then there will be something interesting.
That suggests to us - what if you try to Fibonacci numbers? "Пацан сказал - пацан сделал" (do not know how to translate it to English :).Painted the largest enclosed area.
233х144:



987х610 (pressed 5 times):

As you can see, fractal repeats part of the overall fractal
Fractals, as they are.
Site: New kind of fractals - Fractals in relatively prime integers (coprime integers)
P.S.
And a little bit schizophrenic 11-year-old:
Then, thinking about the relations of chaos and order where chaos is taken in order, and in order - chaos. So that was then thought that when everything exploded (big bang, which I firmly believe), was a ray of electromagnetic energy that is in the early running in a small space (which is further expanded.) Since electromagnetic waves can be in the form of photons - this beam is uninterrupted. Where we see the intersection of electromagnetic waves - there appears the "matter" (https://en.wikipedia.org/wiki/Pair_production) in the form of fractal patterns. Thus is born the order out of chaos.
(2) there is no space in the quantum distance - so there is no common divisor. Always work pattern (what we call matter).
(1) The universe is expanding continuously and smoothly. A fractal is continuous (and also smoothly) goes from one to the other - what we call the motion of matter.
(3). The universe is not two-dimensional and three-dimensional (and from the point of view of the General Theory of Relativity - four-dimensional).
So fractals are much more difficult.
Perhaps the chaos - it is also a fractal?






