- #1
cromata
-Suppose that drop of some fluid ,with which water is miscible, that has higher density than water is dropped in the glass of (still) water.
Forces acting on the drop are gravity and drag force (viscous resistance, Fd=-bv, where v is the velocity of the drop, and b is a constant that depends on the properties of the fluid and the dimensions of the object).
On the micro scale, drag force is caused because water molecules are gaining momentum when they collide with the drop, and thus from the conservation of momentum, momentum (and thus the speed) of the drop has to decline.
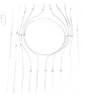
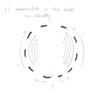
As the the drop is falling through water it becomes flattened because of drag force. This can be explained if we look at the problem from the drops reference frame. In this reference frame, the drop is not moving, and water is moving upwards. Speed of the water is greater on the sides of drop than at the bottom and at the top of the drop. Because of this, static pressure (of water) is greater at the bottom and at the top of the drop and thus, there is force that is squishing the drop.
Explanation why the speed of water is greater on the sides: Suppose that radius of the drop is R, than water molecules that are near the drop travel the distance d≅π*R, and molecules that are far away from drop travel distance d'=2*R. But all those molecules have to arrive at the same hight in same time (if this wasn't not the case then there would be some 'water' missing in some horizontal layer of the water which would cause horizontal movement of water), thus speed has to be greater at the sides of the drop (by approximately factor of π/2).
From the begging of the motion there is vortex motion in drop caused by viscosity. Once drop is flattened, this vortex motion causes the formation of the ring(torus). This is because, circular vortex motion is more stable than elliptic vortex motion (It's sounds intuitive that circular vortex motion is more stable, but can someone explain why would it be more stable on more fundamental level?)
Once the ring is formed, some parts of the ring become more dense. I think this is because the ring is not perfectly symmetric (because of chaotic motion of the fluids).Those parts that are more dense become even more dense because of the cohesive force. Those dense part are heavier than other parts of the ring and because of that they are falling faster than the rest of the ring (drag acceleration is lower for bodies with greater mass adrag =-b/m*v). Eventually those parts break from the ring and become new drops which becomes rings etc. (this is repeated few times, depending on the size of initial drop, temperature of water, drops density etc)
Do you think this model is correct? If not, why?
Here is video of ink drop in water
Similar problem was discussed by J.J Thomson in 19th century and later in 20th century by F. T. Arecchi,P. K. Buah-Bassuah, F Francin and S. Residori
P.S. Sorry for grammar and stylistic mistakes, English is not my native language.
Forces acting on the drop are gravity and drag force (viscous resistance, Fd=-bv, where v is the velocity of the drop, and b is a constant that depends on the properties of the fluid and the dimensions of the object).
On the micro scale, drag force is caused because water molecules are gaining momentum when they collide with the drop, and thus from the conservation of momentum, momentum (and thus the speed) of the drop has to decline.
As the the drop is falling through water it becomes flattened because of drag force. This can be explained if we look at the problem from the drops reference frame. In this reference frame, the drop is not moving, and water is moving upwards. Speed of the water is greater on the sides of drop than at the bottom and at the top of the drop. Because of this, static pressure (of water) is greater at the bottom and at the top of the drop and thus, there is force that is squishing the drop.
Explanation why the speed of water is greater on the sides: Suppose that radius of the drop is R, than water molecules that are near the drop travel the distance d≅π*R, and molecules that are far away from drop travel distance d'=2*R. But all those molecules have to arrive at the same hight in same time (if this wasn't not the case then there would be some 'water' missing in some horizontal layer of the water which would cause horizontal movement of water), thus speed has to be greater at the sides of the drop (by approximately factor of π/2).
From the begging of the motion there is vortex motion in drop caused by viscosity. Once drop is flattened, this vortex motion causes the formation of the ring(torus). This is because, circular vortex motion is more stable than elliptic vortex motion (It's sounds intuitive that circular vortex motion is more stable, but can someone explain why would it be more stable on more fundamental level?)
Once the ring is formed, some parts of the ring become more dense. I think this is because the ring is not perfectly symmetric (because of chaotic motion of the fluids).Those parts that are more dense become even more dense because of the cohesive force. Those dense part are heavier than other parts of the ring and because of that they are falling faster than the rest of the ring (drag acceleration is lower for bodies with greater mass adrag =-b/m*v). Eventually those parts break from the ring and become new drops which becomes rings etc. (this is repeated few times, depending on the size of initial drop, temperature of water, drops density etc)
Do you think this model is correct? If not, why?
Here is video of ink drop in water
Similar problem was discussed by J.J Thomson in 19th century and later in 20th century by F. T. Arecchi,P. K. Buah-Bassuah, F Francin and S. Residori
P.S. Sorry for grammar and stylistic mistakes, English is not my native language.