Frames vs Lines of Simultaneity

[matheinste]

Hi Matheinste.

Since this thread has been left somewhat unresolved I have a question:

Do you think I can assume and state with a degree of confidence that there is no significant difference between a hyperplane and the plane of the frame itself?

Thanks and also for your other input.

I don't understand what you mean by the plane of the frame!

Matheinste.

 

[Austin0]

Hi Matheinste.

Since this thread has been left somewhat unresolved I have a question:

Do you think I can assume and state with a degree of confidence that there is no significant difference between a hyperplane and the plane of the frame itself?

Thanks and also for your other input.

I don't understand what you mean by the plane of the frame!

Matheinste.

The x lines for the rest frame in a 2D Minkowski diagram represent the x-axis or xz plane if you extend it mentally .

Using your rods and clocks analogy [which I use all the time in my mind and have used myself in previous threads] This line represents a line of rods and clocks and virtual observers.
For any point on the worldline this line or plane is limited to the spatial dimension(s)
The clocks all frozen at the same reading. The hyperline (plane) at this moment in time is the exact same rods and clocks. There are no others are there??

This is exactly the same for the sloped hyperline of the moving frame. The same set of rods and clocks as the x'z' plane of the frame.

This has been my understanding and operative assumption for a long time but I did not want to be making statements based on this without checking to see if there was something I was missing or some real difference I was unaware of. SInce so many people seemed to assume they were different I posted this thread to get feedback and other perspectives.

Clearer? Thanks for the feedback it is appreciated

 

[matheinste]

The x lines for the rest frame in a 2D Minkowski diagram represent the x-axis or xz plane if you extend it mentally .

Using your rods and clocks analogy [which I use all the time in my mind and have used myself in previous threads] This line represents a line of rods and clocks and virtual observers.
For any point on the worldline this line or plane is limited to the spatial dimension(s)
The clocks all frozen at the same reading. The hyperline (plane) at this moment in time is the exact same rods and clocks. There are no others are there??

This is exactly the same for the sloped hyperline of the moving frame. The same set of rods and clocks as the x'z' plane of the frame.

This has been my understanding and operative assumption for a long time but I did not want to be making statements based on this without checking to see if there was something I was missing or some real difference I was unaware of. SInce so many people seemed to assume they were different I posted this thread to get feedback and other perspectives.

Clearer? Thanks for the feedback it is appreciated

Having given it more thought I will stick my neck out and say that a network consisting of rods and synchronized clocks with respect to which you are at rest is the same as the hypersurface of simultaneity for the frame of reference in which you are at rest, although I have never seen it described as such and I may receive some adverse comments. However lines and planes of rods and synchronized clocks, although lines ad planes of simultaneity are not the same as the frame of reference but are sections through it.

Matheinste.

 

[Austin0]

Having given it more thought I will stick my neck out and say that a network consisting of rods and synchronized clocks with respect to which you are at rest is the same as the hypersurface of simultaneity for the frame of reference in which you are at rest, although I have never seen it described as such and I may receive some adverse comments. However lines and planes of rods and synchronized clocks, although lines ad planes of simultaneity are not the same as the frame of reference but are sections through it.
Matheinste.

Hi Matheinste Thanks for sticking your neck out and giving me a straight answer.

regarding the second part: Do you mean they are not the reference frame in any sense different from; the lines and planes of that frame as depicted in a diagram are sections through it and not the frame??

Or alternately: Outside the limitations of 2d drawings , as fully 4D constructs would there be any difference in this regard??

Thanks again

 

[matheinste]

regarding the second part: Do you mean they are not the reference frame in any sense different from; the lines and planes of that frame as depicted in a diagram are sections through it and not the frame??

Or alternately: Outside the limitations of 2d drawings , as fully 4D constructs would there be any difference in this regard??

Thanks again

They are not reference frames in the usually defined way as reference frames are usually understood to extend indefinitely in every spatial direction.

In answer to the second part the lower dimensional drawings are limited as you say and so cannot represent reference frames in the usual sense of the word. A reference frame is not a four dimensional construct but three spatial dimensions with clocks added. A snapshot or drawing of a reference frame in three dimensions is a snapshot of the entire spatial extent of space at one particular time. This is a sort of how a reference frame is loosely defined.

Matheinste.

 

[JDoolin]

------------Frames and Lines of Simultaneity----------------

Is there any difference between the two?

If there is what is it??

I may be missing something obvious but as far as I can see they are just two ways of graphing and conceptualizing a singular entity.

Thanks

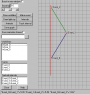
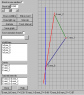
The way I think of it, a simultaneity "Line" "hyper-Plane," or best, "space" of simultaneity can be thought of as whatever is happening "now." Another example is what is happening in the entire universe right "now." And another example is what is happening "NOW." Okay, it sounds like I'm just saying the same thing over and over again, but because I typed them at different times, each one of those is a distinct "space" of simultaneity.

If I were constrained to think in one dimension, then each of those "now"s would have created instead, a "line of simultaneity"

But when I say what is happening "now" of course, I don't mean what I am seeing "now." I will have to wait until the light from faraway events gets here to find out what happened in the universe now. I will die long before I find out what is happening "now" at anything further distant than the most local stars.

On the other hand, when I speak of a frame, I am basically taking all of those "nows" and stacking them up in a flip-book. So you have all of the events, (all of the nows), throughout space and time, as perceived by some hypothetical inertial observer. That is what I would call a "frame."

Opinions may vary.

 

[JesseM]

Just to clarify one thing, when you talk about "frames" do you only mean to talk about inertial frames? Because when it comes to non-inertial frames, specifying what sets of events are simultaneous is not sufficient to tell you which events happen at the same position-coordinate but different times.

 

[JDoolin]

On the other hand, when I speak of a frame, I am basically taking all of those "nows" and stacking them up in a flip-book. So you have all of the events, (all of the nows), throughout space and time, as perceived by some hypothetical inertial observer. That is what I would call a "frame."

Opinions may vary.

After some further thought, I realized I do sometimes use these term frame, when I actually mean "line of simultaneity."

For instance, I might say "That event has not happened yet in his frame" by which I mean that according to his line of simultaneity, the event is in the future.

Or I might say "the events look further apart in this frame, but the actual object is shorter." When I say the events are further apart, I'm talking about the events that occur at different times in the frame, but I say the "actual object" is shorter, and I am talking about where the (events associated with the) object intersects the line of simultaneity.

Jonathan

 

[Austin0]

Just to clarify one thing, when you talk about "frames" do you only mean to talk about inertial frames? Because when it comes to non-inertial frames, specifying what sets of events are simultaneous is not sufficient to tell you which events happen at the same position-coordinate but different times.

Hi I am not sure whether your post was directed to JDoolin or the OP
Just in case I at least was originally talking about inertial frames but I think it would apply generally with the added complications entailed in non-inertial frames.
So what is your take on the original question ? Wrt inertial frames do you see a significant difference between the frame itself and the associated planes of simultaneity??

 

[JDoolin]

Just to clarify one thing, when you talk about "frames" do you only mean to talk about inertial frames? Because when it comes to non-inertial frames, specifying what sets of events are simultaneous is not sufficient to tell you which events happen at the same position-coordinate but different times.

As for me, non-inertial frames seem an ambiguous and ephemeral concept. Some people believe in non-inertial frames; and some people don't, but I don't know if any two people have exactly the same definition. I remain agnostic.

 

[Austin0]

After some further thought, I realized I do sometimes use these term frame, when I actually mean "line of simultaneity."

For instance, I might say "That event has not happened yet in his frame" by which I mean that according to his line of simultaneity, the event is in the future.

Or I might say "the events look further apart in this frame, but the actual object is shorter." When I say the events are further apart, I'm talking about the events that occur at different times in the frame, but I say the "actual object" is shorter, and I am talking about where the (events associated with the) object intersects the line of simultaneity.

Jonathan

Hi Jonathon
Can I infer from this (above) that in the context of this thread you do not see any significant difference between a frame and the lines of simultaneity associated with it?

 

[JDoolin]

Hi Jonathon
Can I infer from this (above) that in the context of this thread you do not see any significant difference between a frame and the lines of simultaneity associated with it?

Ummm. Yes. I should say, more accurately, I have multiple definitions for the term "frame" Maybe I am careless in using the term. But in a sense, when I talk about "what's happening in an inertial reference frame" I'm talking specifically about the events which are occurring at a specific time, and so that implies that I am using the concept of simultaneity, and so those lines must be drawn.

A couple of examples are in order, I suppose. Example 1: If I refer to my car, am I referring to all of the events which have ever, and will ever occur to my car? Am I referring to it in terms of how it appears to someone traveling at .9c? No. I am referring to the car as it is now, in its present state.


Example 2: I've had arguments about this in the past. Some people think that considering the twin paradox in three frames looks like http://upload.wikimedia.org/wikipedia/commons/c/ce/Twin_Paradox_Minkowski_Diagram.svg" :

http://upload.wikimedia.org/wikipedia/commons/c/ce/Twin_Paradox_Minkowski_Diagram.svg

To me, the above link is just a picture of one frame, but someone has drawn in lines if simultaneity for two other frames. If I am discussing the space-time diagram in three different frames, I think you need three different space-time diagrams; one for each frame.

In my mind, a frame should consist of a Cartesian Coordinate system of space, with time progressing in a natural manner from one second to the next. Whereas some people argue that time and space are not necessarily orthogonal, I would argue that it's not really a "frame" until you yoink the space and time axes into their appropriate positions.

Once you've done that, then the "frame" can be said to be but the line of simulteneity representing "now." Just like, when you talk about your car, or your house, or your dog or your cat in the present tense.

Jonathan

 

[Mentz114]

Ummm. Yes. I should say, more accurately, I have multiple definitions for the term "frame" Maybe I am careless in using the term. But in a sense, when I talk about "what's happening in an inertial reference frame" I'm talking specifically about the events which are occurring at a specific time, and so that implies that I am using the concept of simultaneity, and so those lines must be drawn.

[ snip ...]

In my mind, a frame should consist of a Cartesian Coordinate system of space, with time progressing in a natural manner from one second to the next. Whereas some people argue that time and space are not necessarily orthogonal, I would argue that it's not really a "frame" until you yoink the space and time axes into their appropriate positions.

Once you've done that, then the "frame" can be said to be but the line of simultaneity representing "now." Just like, when you talk about your car, or your house, or your dog or your cat in the present tense.

Jonathan

I always thought the lines on a space-time diagram are the worldlines of some thing. Each worldline has a clock and rulers associated with it. That's a frame.

You can show as many worldlines as you want on a diagram, which is the viewpoint of an observer traveling on a vertical worldline. Rotating the diagram can bring any of the worldlines 'to rest', without changing the proper length of any segment of any worldline.

There is no 'now' on the diagram, unless you choose one by drawing a horizontal line, which defines a common parameter time (t) value.

 

[Austin0]

I always thought the lines on a space-time diagram are the worldlines of some thing. Each worldline has a clock and rulers associated with it. That's a frame.

You can show as many worldlines as you want on a diagram, which is the viewpoint of an observer traveling on a vertical worldline. Rotating the diagram can bring any of the worldlines 'to rest', without changing the proper length of any segment of any worldline.

There is no 'now' on the diagram, unless you choose one by drawing a horizontal line, which defines a common parameter time (t) value.

Aren't the horizontal lines for the frame considered at rest assumed to be "now" according to that frames simultaneity and likewise the sloped lines [not the worldline] of the "moving" frame also represent "now" by its conventional simultaneity?
And in both cases this is just an analog of the clocks and ruler of the frame itself.

 

[Mentz114]

Aren't the horizontal lines for the frame considered at rest assumed to be "now" according to that frames simultaneity and likewise the sloped lines [not the worldline] of the "moving" frame also represent "now" by its conventional simultaneity?
And in both cases this is just an analog of the clocks and ruler of the frame itself.

Very likely. 'Now' is a subjective experience and I have never seen it's usefulness.

So I'll keep quiet about it.

 

[Austin0]

Very likely. 'Now' is a subjective experience and I have never seen it's usefulness.

So I'll keep quiet about it.

Too late ,,,you already talked about it even if only to say there was no "now" in a diagram :-)
If I understand you correctly I agree 100%
But can I assume you do think lines of simultaneity for inertial frames are useful for telling local clock relationships at different locations?

 

[Mentz114]

Too late ,,,you already talked about it even if only to say there was no "now" in a diagram :-)
If I understand you correctly I agree 100%

Oh, good. It's a rare thing for anyone to agree with me.

The spacetime diagram shows the past and future of the worldlines. 'Now' is anywhere we choose on a worldline and belongs to that worldline.

But can I assume you do think lines of simultaneity for inertial frames are useful for telling local clock relationships at different locations?

I can't have an opinion on that because I don't understand 'lines of simultaneity'.
Apparently they connect ( light rays ?) events that are simultaneous according to some rule ? But simultaneity is not very meaningful if events are spatially separated is it ?

 

[JDoolin]

Rotating the diagram can bring any of the worldlines 'to rest', without changing the proper length of any segment of any worldline.

I disagree. Rotating the diagram will bring the world-line to a vertical, but the line of simultaneity associated with that worldline gets further away from the horizontal. The way you should bring a world-line "to rest" is a skew operation--not a rotation. You have to pull the line of simultaneity and the world-line in opposite directions.

On the other hand, you say by "rotating" you don't change the proper length. When you are rotating are you also rotating the axes of rotation along with the events? If so, then what you are doing is meaningless. You are turning the diagram to show it to someone else. If you rotate the event coordinates with respect to the x and t axes, you will certainly find that the proper time is not conserved.

There is no 'now' on the diagram, unless you choose one by drawing a horizontal line, which defines a common parameter time (t) value.

There is a difference in the way we think of it that comes clear when I compare your space-time demonstration application to my space-time application.

In your space-time diagram, you have a button that runs the simulation, whereupon you let t go from -10 to +10 and watch the events unfold, as they happen.

In my space-time diagram, on the other hand, upon clicking the "pass-time" button, the computer begins decrementing the time coordinate of every event, so they go from the future, into the present, and then into the past. I have a distinct origin at (0,0) which represents "here and now."

Now both of us use the same origin for the Lorentz Transformation, but in yours, you have an origin that never moves. By decrementing the time coordinate of all of the events over time, I am constantly changing the "now."

It's a difference in convention: for yours, "now" progresses from the negative to the positive. For mine "now" stays at t=0, while the events progress from the future, to the present, to the past.

Jonathan

 

[Mentz114]

I disagree. Rotating the diagram will bring the world-line to a vertical,

by 'rotation' I mean a Lorentz boost. It brings a slanted worldline to the vertical, so we see the scenario from the rest frame of that worldline.

but the line of simultaneity associated with that worldline gets further away from the horizontal. The way you should bring a world-line "to rest" is a skew operation--not a rotation. You have to pull the line of simultaneity and the world-line in opposite directions.

I don't understand what you mean.

On the other hand, you say by "rotating" you don't change the proper length. When you are rotating are you also rotating the axes of rotation along with the events? If so, then what you are doing is meaningless. You are turning the diagram to show it to someone else. If you rotate the event coordinates with respect to the x and t axes, you will certainly find that the proper time is not conserved.

The diagram is turned to show it from the chosen rest frame. As I've said above, a Lorentz transformation is applied. The proper lengths are conserved, as you can see by just reading off the t and x values and calculating t²-x². I've attached a couple of screenshots to demonstrate.

There is a difference in the way we think of it that comes clear when I compare your space-time demonstration application to my space-time application.

In your space-time diagram, you have a button that runs the simulation, whereupon you let t go from -10 to +10 and watch the events unfold, as they happen.

In my space-time diagram, on the other hand, upon clicking the "pass-time" button, the computer begins decrementing the time coordinate of every event, so they go from the future, into the present, and then into the past. I have a distinct origin at (0,0) which represents "here and now."

'here and now' are subjective, and I never could see any use for them. But I think I understand what your app does. It's not the way I'd show events unfolding but I'm sure it makes perfect sense.

Now both of us use the same origin for the Lorentz Transformation, but in yours, you have an origin that never moves. By decrementing the time coordinate of all of the events over time, I am constantly changing the "now."

It's a difference in convention: for yours, "now" progresses from the negative to the positive. For mine "now" stays at t=0, while the events progress from the future, to the present, to the past.

Jonathan

Changing the origin will make no difference to any proper lengths. Nothing moves on a spacetime diagram, if the axes are extended to infinity in all directions, it shows the entire history of the worldlines, from -forever to +forever.

 

[JDoolin]

by 'rotation' I mean a Lorentz boost. It brings a slanted worldline to the vertical, so we see the scenario from the rest frame of that worldline.


I don't understand what you mean.


The diagram is turned to show it from the chosen rest frame. As I've said above, a Lorentz transformation is applied. The proper lengths are conserved, as you can see by just reading off the t and x values and calculating t²-x². I've attached a couple of screenshots to demonstrate.

'here and now' are subjective, and I never could see any use for them. But I think I understand what your app does. It's not the way I'd show events unfolding but I'm sure it makes perfect sense.

Changing the origin will make no difference to any proper lengths. Nothing moves on a spacetime diagram, if the axes are extended to infinity in all directions, it shows the entire history of the worldlines, from -forever to +forever.

Hmmm.

If I have a rotation, my choice of words are rather limited. I can talk of a rotation, or perhaps a revolution. If I am talking about a Lorentz Boost, though, I can call it a Lorentz Transformation, a hyperbolic rotation, an acceleration, a change in velocity, a change in inertial reference frames. Whoever started the habit of calling Lorentz Boost's "rotations" started an unfortunate trend, in my opinion.

As for "here and now" being subjective; that is quite so. In this case "subjective" is not a negative word, but a positive word. Remember, we are talking about relativity, which is essentially the study of subjective measurement. "Here" and "now" are both subjective, and so are "which way is forward; which way is up" and also "how fast and what direction are you going?"

"Here and Now" affects the origin of the diagram
"Which way is forward and which way is up" affects the rotation of the diagram.
"how fast are you going" affects the Lorentz Boost; which determines which world-lines are perpendicular to the lines of simultaneity.

It's all subjective, but it is also all well-defined.

 

[Mentz114]

Hmmm.
If I have a rotation, my choice of words are rather limited. I can talk of a rotation, or perhaps a revolution. If I am talking about a Lorentz Boost, though, I can call it a Lorentz Transformation, a hyperbolic rotation, an acceleration, a change in velocity, a change in inertial reference frames. Whoever started the habit of calling Lorentz Boost's "rotations" started an unfortunate trend, in my opinion.

Mea culpa. I misused 'rotation', but thought it was obvious it was a Lorentz boost. It just looks like a spatial rotation on the diagram.

As for "here and now" being subjective; that is quite so. In this case "subjective" is not a negative word, but a positive word. Remember, we are talking about relativity, which is essentially the study of subjective measurement. "Here" and "now" are both subjective, and so are "which way is forward; which way is up" and also "how fast and what direction are you going?"

"Here and Now" affects the origin of the diagram
"Which way is forward and which way is up" affects the rotation of the diagram.
"how fast are you going" affects the Lorentz Boost; which determines which world-lines are perpendicular to the lines of simultaneity.

It's all subjective, but it is also all well-defined.

Fine, I have no problem with that.

 

[JDoolin]

You may have seen these before, but there are a couple good graphics showing the visual difference between rotation transformation and Lorentz Transformation on http://casa.colorado.edu/~ajsh/sr/wheel.html" .

And there's the http://commons.wikimedia.org/wiki/File:Animated_Lorentz_Transformation.gif" at Wikipedia, which was inspired, partially, by Andrew Hamilton's work.

And, of course, your demo does it too. Here, I've attached a file called "here and now axes." Load the project into your Minkowski program. There are three events to the left, three events to the right, three events in the future, and three events in the past, and an origin.

Put in a boost by .01 and hit the boost button several times. You should see how the line of simultaneity (horizontal) rotates counterclockwise, in the opposite direction from the world-line (vertical).

 

[Mentz114]

You may have seen these before, but there are a couple good graphics showing the visual difference between rotation transformation and Lorentz transformation on Andrew Hamilton's website.

Please, I may have erred by using 'rotation' to describe the LT in my program, but I do know the difference.

And, of course, your demo does it too. Here, I've attached a file called "here and now axes." Load the project into your Minkowski program. There are three events to the left, three events to the right, three events in the future, and three events in the past, and an origin.

That's interesting. I haven't seen that done. It looks as if the axes are transforming when the events are boosted. I'll have to think about that.

[later]Aha. The events along the x-axis all happen simultaneously in the rest frame of the diagram. When it's boosted, so we're now viewing the events from a moving frame, they are no longer simultaneous. Cool. It illustrates the relativity of simultaneity.

The events on the t-axis all happen in the same place but at different times, in the rest frame of the diagram. Boosted, they now appear to happen in different places, with different intervals. Doppler effect ?

 

[Austin0]

If I understand you correctly I agree 100%

Oh, good. It's a rare thing for anyone to agree with me.

I find that hard to believe

The spacetime diagram shows the past and future of the worldlines. 'Now' is anywhere we choose on a worldline and belongs to that worldline.

Of course ,,,and whatever point you choose on the worldline** has attached a line of simultaneity which graphs the position and times [of the colocated clocks in the other frame] of all the clocks in that** frame that are simultaneously [ a conventional assumption] reading the same proper time.
Would yu agree?

But can I assume you do think lines of simultaneity for inertial frames are useful for telling local clock relationships at different locations?

I can't have an opinion on that because I don't understand 'lines of simultaneity'.

Well as far as I can see they are just the ruler and clocks of the frame itself. Extended in space so if the range exceeds the actual physical bounds of the frame's ruler it is extended by a virtual ruler with clocks and observers. This is exactly the point of the OP

Apparently they connect ( light rays ?) events that are simultaneous according to some rule ? But simultaneity is not very meaningful if events are spatially separated is it ?

Yes we are agreed that simultaneity has no real meaning regarding spatially separated events.
But it does have objective meaning as far as predicting local [colocal] clock relationships between inertial frames. That both frames will always agree regarding these local events. Make sense??

 

[Mentz114]

Make sense??

As I've said I have no quibble with the way you see things, I just have a different POV.

 

[JDoolin]

Please, I may have erred by using 'rotation' to describe the LT in my program, but I do know the difference.



That's interesting. I haven't seen that done. It looks as if the axes are transforming when the events are boosted. I'll have to think about that.

[later]Aha. The events along the x-axis all happen simultaneously in the rest frame of the diagram. When it's boosted, so we're now viewing the events from a moving frame, they are no longer simultaneous. Cool. It illustrates the relativity of simultaneity.

The events on the t-axis all happen in the same place but at different times, in the rest frame of the diagram. Boosted, they now appear to happen in different places, with different intervals. Doppler effect ?

:) Cool

Maybe not the Doppler effect. Maybe the "relativity of simultaneity." I prefer to call it "desynchronization" but that's never caught on.

My perception has been that most of the time I've encountered people who talk about the Relativistic Doppler effect, they are just talking about a more precise means to calculate redshift and blueshift. They may or may not be aware of the relativity of simultaneity.

If your idea of the Doppler effect involves an elongated version of the object coming toward you superluminally, with a high blue-shift, and then a shortened red-shifted version of the object, receding from you by, then yes, it's the Relativistic Doppler effect.

However, this phenomenon is already called by another name; Penrose http://en.wikipedia.org/wiki/Terrell_rotation" .

 

[Austin0]

As I've said I have no quibble with the way you see things, I just have a different POV.

Likewise. I am just not really sure rnough of your POV to even know if there is any disagreement whatsoever. You have said you don't understand lines of simultaneity, but judging by your other posts it appears you are fully knowledgeable in all aspects. So?
But no worries

 

[Austin0]

:) Cool

Maybe not the Doppler effect. Maybe the "relativity of simultaneity." I prefer to call it "desynchronization" but that's never caught on.

My perception has been that most of the time I've encountered people who talk about the Relativistic Doppler effect, they are just talking about a more precise means to calculate redshift and blueshift. They may or may not be aware of the relativity of simultaneity.

If your idea of the Doppler effect involves an elongated version of the object coming toward you superluminally, with a high blue-shift, and then a shortened red-shifted version of the object, receding from you by, then yes, it's the Relativistic Doppler effect.

However, this phenomenon is already called by another name; Penrose http://en.wikipedia.org/wiki/Terrell_rotation" .

Desynchronization is fine with me. But what do you mean by "superluminally"

and I am fairly sure The Penrose-Terrell effect is a purely visual distortion as a consequence of the finite propagation speed of light and different path lengths from various parts of an object to the POV
cheers

 

[JDoolin]

Desynchronization is fine with me. But what do you mean by "superluminally"

and I am fairly sure The Penrose-Terrell effect is a purely visual distortion as a consequence of the finite propagation speed of light and different path lengths from various parts of an object to the POV
cheers

http://en.wikipedia.org/wiki/Superluminal_motion

Superluminal motion, the Penrose Terrell effect and the Relativistic Doppler effect are all three purely visual distortions as a consequence of the finite propagations speed of light.

...and I overgeneralized: The relativistic Doppler effect won't cause superluminal motion for small velocities of course.

Jonathan