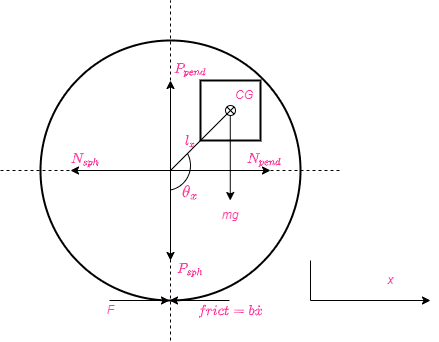
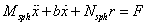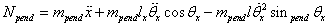Thank you! Unfortunately, the task is formulated not in English, so I can’t simply quote it. It's kind of an inverted pendulum on a cart problem. But only instead of a cart, the pendulum is attached to the motor shaft that is placed in the centre of the spherical enclosure. Consequently, by changing the inclination of the pendulum one can make the sphere move and vice versa. I shall determine the position of the sphere in a two-dimensional plane in dependence on the inclination of the pendulum.
In the diagram, I’ve used the next notations:
CG - centre of gravity;
theta - inclination of the pendulum;
lx - distance between the centre of the sphere and the centre of gravity;
Npend - reaction force of the pendulum and Nsph is corresponding reaction of the sphere
P - force of gravity.
And the symbols in equations are:
mpend - mass of the pendulum;
Msph - mass of the spherical enclosure;
x - displacement of the spherical body;
r - radius of the sphere;
b - friction coefficient.