kps
- 5
- 1
Hoping someone can chip in and help me understand a problem when it comes to two-force members.
I have a structure as shown below. Essentially its a single body attached at 3 points with pin joints. My question is, is it appropriate to treat each of the left and right side as individual members, making them single two-force members and therefore have a reaction force in x AND y, at both point 2 and 3. Or is the fact that it's a single rigid body mean it can't be a two force member and there will only be a y reaction force at 2 and 3.
Many thanks!
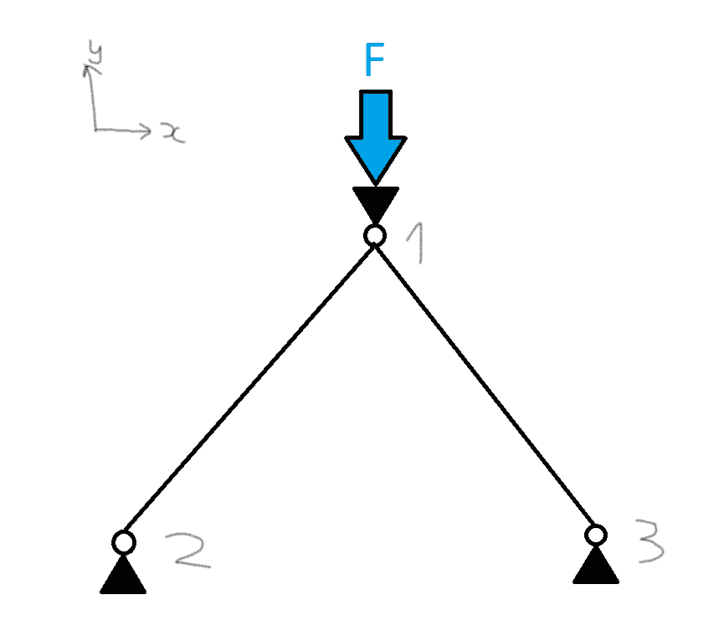
I have a structure as shown below. Essentially its a single body attached at 3 points with pin joints. My question is, is it appropriate to treat each of the left and right side as individual members, making them single two-force members and therefore have a reaction force in x AND y, at both point 2 and 3. Or is the fact that it's a single rigid body mean it can't be a two force member and there will only be a y reaction force at 2 and 3.
Many thanks!
 ##\qquad## !
##\qquad## !