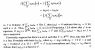- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading Paul E. Bland's book, "Rings and Their Modules".
I am trying to understand Section 2.2 on free modules and need help with the proof of Corollary 2.2.4.
Corollary 2.2.4 and its proof read as follows:

 In the second last paragraph of Bland's proof above we read:
In the second last paragraph of Bland's proof above we read:
" ... ... If [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex], then [itex] \sum_\Delta x_\alpha a_\alpha \in F [/itex] ... ... "My question is as follows:
How, exactly, do we know that [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] implies that [itex]\sum_\Delta x_\alpha a_\alpha \in F[/itex] ... ... that is, is it possible that for some [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] there is no element [itex]x [/itex] such that [itex]x = \sum_\Delta x_\alpha a_\alpha \in F [/itex]?To make sure my question is clear ... ...
If F is a free R-module with basis [itex]\{ x_\alpha \}_\Delta [/itex], then every element [itex]x \in F[/itex] can be expressed (generated) as a sum of the form:
[itex]x = \sum_\Delta x_\alpha a_\alpha [/itex]
... ... BUT ... ... does this mean that for any element [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] there is actually an element [itex]x \in F[/itex] such that [itex]x = \sum_\Delta x_\alpha a_\alpha [/itex]?
... OR ... to put it another way ... could it be that for some element [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] there is actually NO element [itex]x \in F[/itex] such that [itex]x = \sum_\Delta x_\alpha a_\alpha [/itex]?
Can someone please clarify this issue for me?
Peter
***NOTE***I thought I would try to clarify just exactly why I am perplexed about the nature of the generation of a module or submodule by a set [itex]S[/itex].
Bland defines the generation of a submodule of [itex]N[/itex] of an [itex]R[/itex]-module [itex]M[/itex] as follows:
 Now consider a submodule [itex]L[/itex] of [itex]M[/itex] such that [itex]L \subset N[/itex].
Now consider a submodule [itex]L[/itex] of [itex]M[/itex] such that [itex]L \subset N[/itex].
See Figure [itex]1[/itex] as follows:

Now [itex]L[/itex], like [itex]N[/itex], will (according to Bland's definition) also be generated by [itex]S[/itex], since every element [itex]y \in L[/itex] will be able to be expressed as a sum
[itex]y = \sum_{\Delta} x_\alpha a_\alpha
[/itex]
where [itex]x_\alpha \in S [/itex] and [itex]a_\alpha \in R[/itex]
This is possible since every element of [itex]N[/itex] (and hence [itex]L[/itex]) can be expressed this way.However ... ... if we consider [itex]x \in N[/itex] such that [itex]x \notin L[/itex] then
[itex]x = \sum_{\Delta} x_\alpha a_\alpha
[/itex]
for some [itex]x_\alpha, a_\alpha
[/itex]
... ... BUT ... ... in this case, there is no [itex](a_\alpha) \in R^{ ( \Delta ) } [/itex] such that
[itex] \sum_{\Delta} x_\alpha a_\alpha \in L [/itex]
... ... BUT ... ... this is what is assumed in Bland's proof of Corollary [itex]2.2.4[/itex]?
Can someone please clarify this issue ...
Peter
I am trying to understand Section 2.2 on free modules and need help with the proof of Corollary 2.2.4.
Corollary 2.2.4 and its proof read as follows:
" ... ... If [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex], then [itex] \sum_\Delta x_\alpha a_\alpha \in F [/itex] ... ... "My question is as follows:
How, exactly, do we know that [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] implies that [itex]\sum_\Delta x_\alpha a_\alpha \in F[/itex] ... ... that is, is it possible that for some [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] there is no element [itex]x [/itex] such that [itex]x = \sum_\Delta x_\alpha a_\alpha \in F [/itex]?To make sure my question is clear ... ...
If F is a free R-module with basis [itex]\{ x_\alpha \}_\Delta [/itex], then every element [itex]x \in F[/itex] can be expressed (generated) as a sum of the form:
[itex]x = \sum_\Delta x_\alpha a_\alpha [/itex]
... ... BUT ... ... does this mean that for any element [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] there is actually an element [itex]x \in F[/itex] such that [itex]x = \sum_\Delta x_\alpha a_\alpha [/itex]?
... OR ... to put it another way ... could it be that for some element [itex](a_\alpha) \in R^{ ( \Delta ) }[/itex] there is actually NO element [itex]x \in F[/itex] such that [itex]x = \sum_\Delta x_\alpha a_\alpha [/itex]?
Can someone please clarify this issue for me?
Peter
***NOTE***I thought I would try to clarify just exactly why I am perplexed about the nature of the generation of a module or submodule by a set [itex]S[/itex].
Bland defines the generation of a submodule of [itex]N[/itex] of an [itex]R[/itex]-module [itex]M[/itex] as follows:
See Figure [itex]1[/itex] as follows:
Now [itex]L[/itex], like [itex]N[/itex], will (according to Bland's definition) also be generated by [itex]S[/itex], since every element [itex]y \in L[/itex] will be able to be expressed as a sum
[itex]y = \sum_{\Delta} x_\alpha a_\alpha
[/itex]
where [itex]x_\alpha \in S [/itex] and [itex]a_\alpha \in R[/itex]
This is possible since every element of [itex]N[/itex] (and hence [itex]L[/itex]) can be expressed this way.However ... ... if we consider [itex]x \in N[/itex] such that [itex]x \notin L[/itex] then
[itex]x = \sum_{\Delta} x_\alpha a_\alpha
[/itex]
for some [itex]x_\alpha, a_\alpha
[/itex]
... ... BUT ... ... in this case, there is no [itex](a_\alpha) \in R^{ ( \Delta ) } [/itex] such that
[itex] \sum_{\Delta} x_\alpha a_\alpha \in L [/itex]
... ... BUT ... ... this is what is assumed in Bland's proof of Corollary [itex]2.2.4[/itex]?
Can someone please clarify this issue ...
Peter