Free particle: Quantum and Classical treatment

[Abdul Quader]

I have a problem finding $\left|Ψ(x,t)\right|^2$ from the following equation:

$$Ψ(x,t) = \frac 1 {\pi \sqrt{2a}} \int_{-∞}^{+∞} \frac {\sin(ka)} k e^{i(kx - \frac {ħk^2} {2m} t)} dk$$

and tried to plot like the pic below (Source Introduction to quantum mechanics by David. J. Griffiths, 2nd Edition, page 75). I need help finding $\left|Ψ(x,t)\right|^2$.

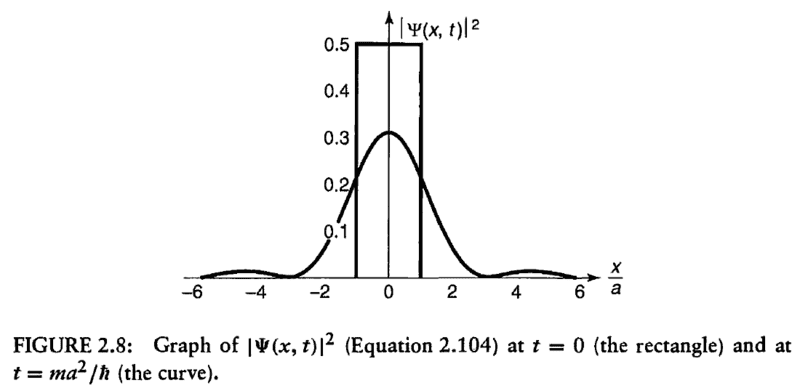
Does understanding Plancherel's theorem helps understanding the expression of wave packet as follows?
$$Ψ(x,t) = \frac 1 {\sqrt{2\pi}} \int_{-∞}^{+∞} \phi(k) e^{i(kx - \frac {ħk^2} {2m} t)} dk$$

I didn't understand how Griffiths arrived at that expression. Thanks in advance.

 

[BvU]

On thing at a time. What expresssion do you have for $|\Psi(x,t)|^2$ ?

 

[Abdul Quader]

On thing at a time. What expresssion do you have for $|\Psi(x,t)|^2$ ?

Do I calculate something like this?

$|Ψ(x,t)|^2 = (\frac 1 {\sqrt{2\pi}} \int_{-∞}^{+∞} \phi(k)e^{i(kx - \frac {ħk^2}{2m}t)}dk)(\frac 1 {\sqrt{2\pi}} \int_{-∞}^{+∞} \phi(k)e^{-i(kx - \frac {ħk^2}{2m}t)}dk)$

I don't know how to do this.

 

[BvU]

You rename one of the two integration variables to $k'$ or something and try to merge the two integrals, perhaps ?

( in the griffiths 1995 I have here, your $\phi(k)$ expression is the outcome of problem 2.21b on page 50, but he doesn't ask any further, just: "(c) Comment on the behaviour of $\phi(k)$ for very small and very large values of a." )

 

[BvU]

I am starting to feel quite uneasy about this one: the curve in fig 2.8 looks a lot like $|\phi(k)|^2_{t=0}$ and I find it hard to believe $|\Psi(x)|^2_{t=...}$ should have the same shape (the only one that is its own Fourier transform is the gaussian). What does eq 2.104 look lke ?
Can @Orodruin shed some light on this ?

 

[vanhees71]

Well, Griffiths's QM book again. I'm not sure what Griffiths wants to explain with this, but it's pretty obvious concerning the math.

For free particles the momentum eigenstates are at the same time energy eigenstates and thus the most convenient way to solve the time-dependent Schrödinger equation. In the following for convenience, I set $\hbar=1$. Griffiths starts with the initial condition in position space,
$$\Psi_0(x)=\Psi(x,0)=\frac{1}{\sqrt{2 a}} \Theta(-a<x<a),$$
i.e. the box graph in the figure (he plots $|\Psi|^2$ though).

The momentum-space representation of this initial wave function is found by taking its Fourier transform,
$$\tilde{\Psi}_0(p)=\frac{1}{\sqrt{2 \pi}} \int_{\mathbb{R}} \mathrm{d} x \Psi_0(x) \exp(-\mathrm{i} p x) = \frac{1}{\sqrt{4 \pi a}} \int_{-a}^{a} \mathrm{d} x \exp(-\mathrm{i} p x) =\frac{\mathrm{1}}{\sqrt{\pi a}} \frac{\sin(a p)}{p}.$$
Now you get the time evolution in the Schrödinger picture by using
$$|\Psi,t \rangle \rangle = \exp(-\mathrm{i} t \hat{H}) |\Psi_0 \rangle=\exp[-\mathrm{i} t \hat{p}^2/(2m) ]|\Psi_0 \rangle.$$
To get the wave function, you have to multiply this with $\langle x|$ from the left and then use the completeness relation of the (generalized) momentum eigenstates:
$$\Psi(t,x)=\langle x|\exp[-\mathrm{i} t p^2/(2m)]|\Psi_0 \rangle = \int_{\mathbb{R}} \mathrm{d} p \langle x|\exp[-\mathrm{i} t \hat{p}^2/(2m)]|p \rangle \langle p|\Psi_0 \rangle=\int_{\mathbb{R}} \mathrm{d} p \langle x|p \rangle \exp[\mathrm{i} t p^2/(2m)] \langle p|\Psi_0 \rangle = \frac{1}{\sqrt{2 a} \pi} \int_{\mathbb{R}}\mathrm{d} p \exp \left [\mathrm{i} \left (p x-\frac{p^2 t}{2m} \right) \right] \frac{\sin(a p)}{p},$$
which is the given expression.

 

[BvU]

Thanks. However, this time development expression of the Fourier transformed $\Psi(x, 0)$ is the starting equation in post #1.
Abdul and I will need further help to bring this to a $\operatorname{ sinc}^2$ form for $|\Psi(x,t)|^2$ at $\ t = ma^2/\hbar\$ as Grif sketches in the figure ...

 

[vanhees71]

Well that's a pretty tough calculation, even with help of mathematica. Doing the integral directly doesn't give a very helpful result in Mathematica. The trick is to first calculate the derivative of the wave function, which gives a Gaussian integral:
$$\partial_x \Psi(t,x) = \sqrt{\frac{m}{4 \pi a \mathrm{i} t}} \left [\exp \left (\frac{\mathrm{i} m (a+x)^2}{2 t} \right) - \exp \left (\frac{\mathrm{i} m (a-x)^2}{2 t} \right) \right].$$
Integrating wrt. $x$ then gives
$$\Psi(t,x)=-\frac{\mathrm{i}}{\sqrt{8 a}}\left [\text{erfi} \left (\frac{\sqrt{\mathrm{i} m}(a+x)}{\sqrt{2 t}} \right ) + \text{erfi} \left (\frac{\sqrt{\mathrm{i} m}(a-x)}{\sqrt{2 t}} \right ) \right].$$
For the definition of the imaginary error integral, see

http://mathworld.wolfram.com/Erfi.html

 

[Abdul Quader]

I am starting to feel quite uneasy about this one: the curve in fig 2.8 looks a lot like $|\phi(k)|^2_{t=0}$ and I find it hard to believe $|\Psi(x)|^2_{t=...}$ should have the same shape (the only one that is its own Fourier transform is the gaussian). What does eq 2.104 look lke ?
Can @Orodruin shed some light on this ?

The first equation I have written in the original post is the equation 2.104. Sorry to reply so late.

 

[BvU]

Ok, so the caption of fig 2.8 is misleading: it says $|\Psi(x,t)|^2$ but refers to an integral form for $\Psi(x,t)$.

Did some googling and found The evolution of free wave packets by Mark Andrews (Australian National University), where the second example, figure 3, is interesting !

It shows that all the violence associated with the higher frequencies fades out very rapidly and well before $\ t = ma^2/\hbar\$ the shape is like Griffiths draws it.

Moreover, it does all the math (and to me it looks like a lot... ) that I asked for in #7, including the calculation of an error bound.
And my uneasiness as expressed in #5 turns out to be unnecessary: his equation (31) is indeed a $\operatorname{ sinc}^2\$ !

Thanks to Abdul for putting question marks with a loose treatment in the book and thus pointing at an interesting case.

And thanks to @vanhees71 for his contributions.
$\mathstrut$

And I notice Grif has changed the exercise 2.21 at some point between 1995 and 2005: the solutions manual deals with a $\Psi(x,0) = Ae^{-ax}$ instead of a constant $A$ for $-a<x<a$

[edit]oops, yes: $\Psi(x,0) = Ae^{-a|x|}$

$\mathstrut$

 

[vanhees71]

But $\Psi(x,0)=A \exp(-a x)$ cannot be a proper wave function, since it's not square integrable. A much nicer example, which you can calculate in terms of elementary functions is the Gaussian wave packet, i.e.,
$$\Psi(x,0)=A \exp(-x^2/a^2+\mathrm{i} k_0 x).$$
It's a nice exercise of Fouriertransormations of Gaussian functions ;-)). Have fun!

 

[George Jones]

And I notice Grif has changed the exercise 2.21 at some point between 1995 and 2005: the solutions manual deals with a $\Psi(x,0) = Ae^{-ax}$ instead of a constant $A$ for $-a<x<a$

But $\Psi(x,0)=A \exp(-a x)$ cannot be a proper wave function, since it's not square integrable. A much nicer example, which you can calculate in terms of elementary functions is the Gaussian wave packet, i.e.,
$$\Psi(x,0)=A \exp(-x^2/a^2+\mathrm{i} k_0 x).$$
It's a nice exercise of Fouriertransormations of Gaussian functions ;-)). Have fun!

In Problem 2.21 (of the second edition, 2005),
$$\Psi \left(x,0\right) = \exp\left(-a \left|x\right|\right) .$$
A Gaussian wave packet is the subject of Problem 2.22.

 

[vanhees71]

Of course, with the modulus it's a fine initial state.