- #1
fisher garry
- 63
- 1
$$\textbf{F} \cdot d\textbf{l}=q(\textbf{E}+\textbf{v} \times \textbf{B})\cdot \textbf{v} dt$$
If we denote $$q=\rho d \tau$$ and $$\rho \textbf{v}=\textbf{J}$$
$$\frac{dW}{dt}=\int_{V} (\textbf{E} \cdot \textbf{J}) d \tau.$$
From maxwell law's
$$\textbf{E} \cdot \textbf{J}=\frac{1}{\mu _0} \textbf{E} \cdot (\nabla \times \textbf{B}) - \epsilon _0 \textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t}
$$
we use the product rule:
$$\nabla \dot \cdot (\textbf{E} \times \textbf{B})=\textbf{B} \cdot (\nabla \times \textbf{E})-\textbf{E} \cdot (\nabla \times \textbf{B}).$$
Faraday's law:
$$\nabla \times \textbf{E}=-\frac{\partial \textbf{B}}{\partial t}
$$
gives
$$\textbf{E} \cdot (\nabla \times \textbf{B})=-\frac{\partial \textbf{B}}{\partial t} - \nabla \cdot (\textbf{E} \times \textbf{B})
$$
$$\textbf{B} \cdot \frac{\partial \textbf{B}}{\partial t}=\frac{1}{2} \frac{\partial}{\partial t}(B^2)$$
$$\textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t}=\frac{1}{2} \frac{\partial}{\partial t}(B^2)$$
$$\textbf{E} \cdot \textbf{J}=\frac{1}{2} \frac{\partial}{\partial t}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) - \frac{1}{\mu_0} \nabla \cdot (\textbf{E} \times \textbf{B}).$$
The theory above is taken from Griffiths introduction to electrodynamics.
From there by rearranging:
$$\textbf{F} \cdot d \textbf{l}=\frac{q}{\rho}[-\frac{1}{2} \frac{\partial}{\partial t}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) - \frac{1}{\mu_0} \nabla \cdot (\textbf{E} \times \textbf{B})] dt$$
From a quantification perspective we could rewrite the last part to:
$$\textbf{F} \cdot d \textbf{l}=\frac{q}{\rho}[-\frac{1}{2} \frac{\partial}{\partial t}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) - \frac{1}{\mu_0}c \nabla \cdot ( \textbf{B}^2) ] dt$$$$\frac{d W}{d t}=\frac{q}{\rho}[-\frac{1}{2} \frac{\partial}{\partial t}\int_{V}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) d \tau - \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau$$
The first term is recognized as the energy density. If all the energy is sent out instead of stored in the system:
$$\frac{d W}{d t}= \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau$$
From the divergence theorem:
$$\frac{d W}{d t}= \frac{c}{\mu_0}\int_{A} \textbf{B}^2 \cdot dA=\frac{c}{\mu_0} \textbf{B}^2 4 \pi r^2 $$
If we denote this emitted energy as Em waves:
$$B=\textbf{B} \sin [2 \pi ft]$$
$$W=\frac{c}{\mu_0} \textbf{B}^2 \int_{0}^{T} \sin^2[2 \pi ft] 4 \pi r^2 dt$$
$$\sin^2x=\frac{1}{2}-\cos(2x)$$
$$W=\frac{c}{\mu_0} \textbf{B}^2 \int_{0}^{T}(\frac{1}{2}-\cos([4 \pi ft]) 4 \pi r^2 )dt=\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
From another approach of the theory in Griffiths:
Again we look at the energy sent out and assume that no energy is stored
$$\frac{d W}{d t}= \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau$$
Now instead of using the divergence theorem there could perhaps be possible to do this volume integral above and then equate it to:
$$\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
And then solve for $$T=\frac{1}{f}$$
What I have done so far:
We assume that B goes radially outwards and use spherical coordinates to solve the divergence theorem:
The divergence in spherical coordinates:
$$\frac{1}{r^2} \frac{\partial r^2 A_r}{\partial r} + \frac{1}{r sin \theta}\frac{\partial}{\partial \theta}A_{\theta}sin_{\theta} + \frac{1}{r sin \theta} \frac{\partial A_{\varphi}}{ \partial \varphi}$$
Since we only have radial divergence we can obtain:
$$\frac{d W}{d t}= \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau=\frac{c}{\mu_0}\int_{V} \frac{1}{r^2} \frac{d}{dr}(r^2B^2)4 \pi r^2 dr=\frac{4 \pi c}{\mu_0}\int_{0}^r d (r^2B^2)=\frac{4 \pi c}{\mu_0} (r^2B^2)$$
Which we see is the same result as we ended up with above as:
$$W=\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
But what if we instead tried to integrate
$$\frac{c}{\mu_0}\int_{V} \frac{1}{r^2} \frac{d}{dr}(r^2B^2)4 \pi r^2 dr$$
by rewriting:
$$B=\textbf{B} \sin [2 \pi ft]=\textbf{B} \sin [2 \pi f\frac{r}{c}]$$
Thus
$$\frac{c}{\mu_0}\int_{V} \frac{1}{r^2} \frac{d}{dr}(r^2\textbf{B}^2 \sin^2 [2 \pi f\frac{r}{c}])4 \pi r^2 dr$$
Then we have a r dependency for the integral. I have tried and I ended up with a longer expression. The better news was that if I equated it with
$$\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
I ended up with an equation that only had R and f as variables since B is the same for the two divergence theorems versions from the derivations above. I guess I could initially determine R from a setup point of view. But unfortunately it did not give any solutions. It seems that since there are 2 Work equations. Equating thoose two could give a solution of frequency. But I have not found a solution that makes sense. Anyone that wants to try to find a solution for the frequency with this setup?
Here is my attempt attached just in case anyone want to take a look (the answer gave me 0 answers as far as I could tell):
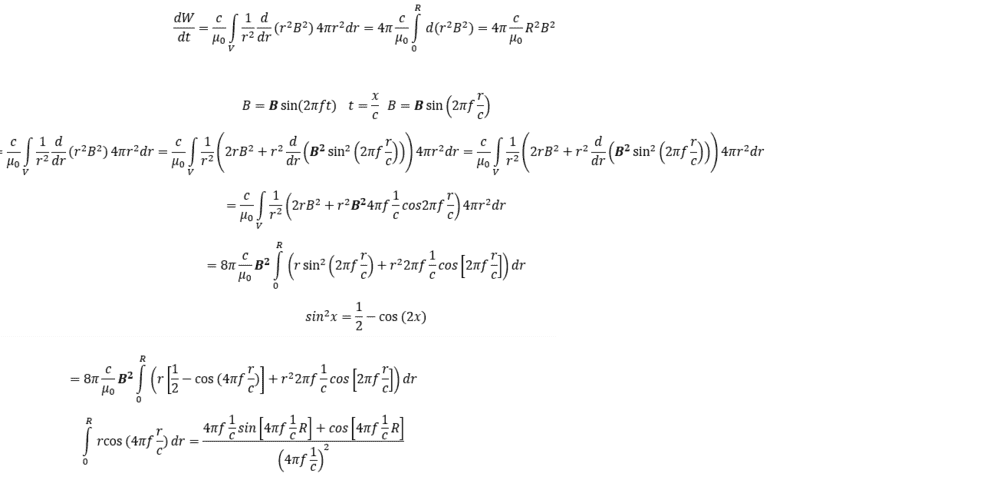
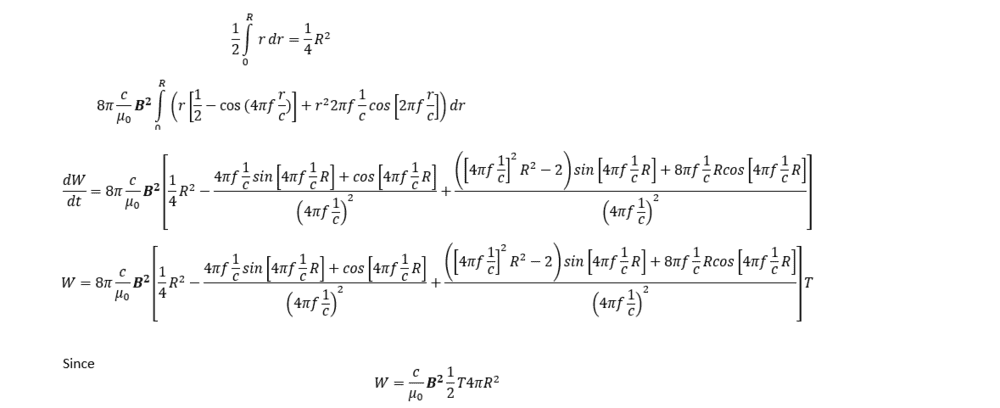
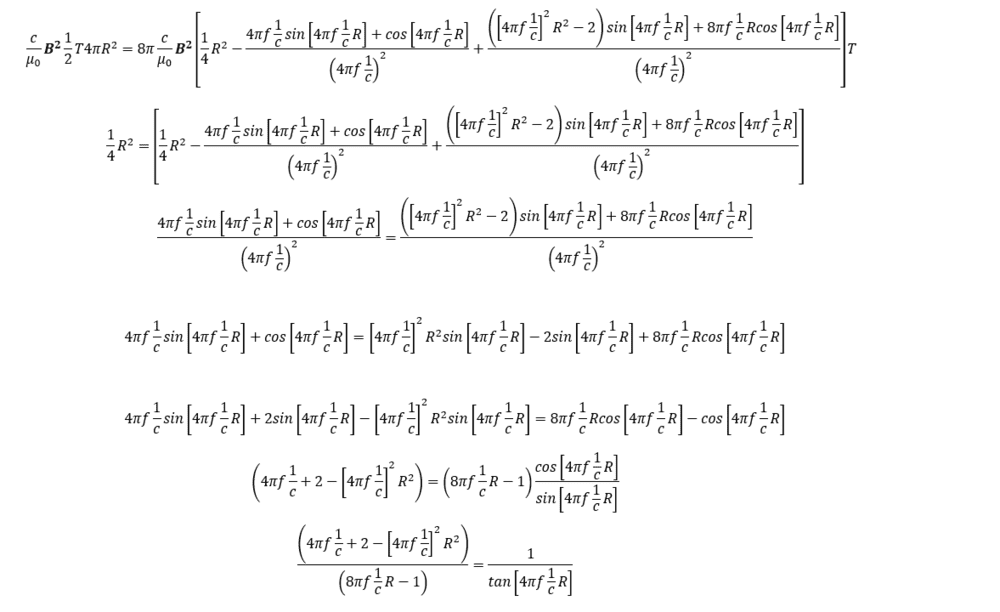
If we denote $$q=\rho d \tau$$ and $$\rho \textbf{v}=\textbf{J}$$
$$\frac{dW}{dt}=\int_{V} (\textbf{E} \cdot \textbf{J}) d \tau.$$
From maxwell law's
$$\textbf{E} \cdot \textbf{J}=\frac{1}{\mu _0} \textbf{E} \cdot (\nabla \times \textbf{B}) - \epsilon _0 \textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t}
$$
we use the product rule:
$$\nabla \dot \cdot (\textbf{E} \times \textbf{B})=\textbf{B} \cdot (\nabla \times \textbf{E})-\textbf{E} \cdot (\nabla \times \textbf{B}).$$
Faraday's law:
$$\nabla \times \textbf{E}=-\frac{\partial \textbf{B}}{\partial t}
$$
gives
$$\textbf{E} \cdot (\nabla \times \textbf{B})=-\frac{\partial \textbf{B}}{\partial t} - \nabla \cdot (\textbf{E} \times \textbf{B})
$$
$$\textbf{B} \cdot \frac{\partial \textbf{B}}{\partial t}=\frac{1}{2} \frac{\partial}{\partial t}(B^2)$$
$$\textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t}=\frac{1}{2} \frac{\partial}{\partial t}(B^2)$$
$$\textbf{E} \cdot \textbf{J}=\frac{1}{2} \frac{\partial}{\partial t}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) - \frac{1}{\mu_0} \nabla \cdot (\textbf{E} \times \textbf{B}).$$
The theory above is taken from Griffiths introduction to electrodynamics.
From there by rearranging:
$$\textbf{F} \cdot d \textbf{l}=\frac{q}{\rho}[-\frac{1}{2} \frac{\partial}{\partial t}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) - \frac{1}{\mu_0} \nabla \cdot (\textbf{E} \times \textbf{B})] dt$$
From a quantification perspective we could rewrite the last part to:
$$\textbf{F} \cdot d \textbf{l}=\frac{q}{\rho}[-\frac{1}{2} \frac{\partial}{\partial t}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) - \frac{1}{\mu_0}c \nabla \cdot ( \textbf{B}^2) ] dt$$$$\frac{d W}{d t}=\frac{q}{\rho}[-\frac{1}{2} \frac{\partial}{\partial t}\int_{V}(\epsilon_0 E^2+\frac{1}{\mu_0} B^2) d \tau - \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau$$
The first term is recognized as the energy density. If all the energy is sent out instead of stored in the system:
$$\frac{d W}{d t}= \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau$$
From the divergence theorem:
$$\frac{d W}{d t}= \frac{c}{\mu_0}\int_{A} \textbf{B}^2 \cdot dA=\frac{c}{\mu_0} \textbf{B}^2 4 \pi r^2 $$
If we denote this emitted energy as Em waves:
$$B=\textbf{B} \sin [2 \pi ft]$$
$$W=\frac{c}{\mu_0} \textbf{B}^2 \int_{0}^{T} \sin^2[2 \pi ft] 4 \pi r^2 dt$$
$$\sin^2x=\frac{1}{2}-\cos(2x)$$
$$W=\frac{c}{\mu_0} \textbf{B}^2 \int_{0}^{T}(\frac{1}{2}-\cos([4 \pi ft]) 4 \pi r^2 )dt=\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
From another approach of the theory in Griffiths:
Again we look at the energy sent out and assume that no energy is stored
$$\frac{d W}{d t}= \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau$$
Now instead of using the divergence theorem there could perhaps be possible to do this volume integral above and then equate it to:
$$\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
And then solve for $$T=\frac{1}{f}$$
What I have done so far:
We assume that B goes radially outwards and use spherical coordinates to solve the divergence theorem:
The divergence in spherical coordinates:
$$\frac{1}{r^2} \frac{\partial r^2 A_r}{\partial r} + \frac{1}{r sin \theta}\frac{\partial}{\partial \theta}A_{\theta}sin_{\theta} + \frac{1}{r sin \theta} \frac{\partial A_{\varphi}}{ \partial \varphi}$$
Since we only have radial divergence we can obtain:
$$\frac{d W}{d t}= \frac{1}{\mu_0}\int_{V}c \nabla \cdot ( \textbf{B}^2) \textbf{i}] d\tau=\frac{c}{\mu_0}\int_{V} \frac{1}{r^2} \frac{d}{dr}(r^2B^2)4 \pi r^2 dr=\frac{4 \pi c}{\mu_0}\int_{0}^r d (r^2B^2)=\frac{4 \pi c}{\mu_0} (r^2B^2)$$
Which we see is the same result as we ended up with above as:
$$W=\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
But what if we instead tried to integrate
$$\frac{c}{\mu_0}\int_{V} \frac{1}{r^2} \frac{d}{dr}(r^2B^2)4 \pi r^2 dr$$
by rewriting:
$$B=\textbf{B} \sin [2 \pi ft]=\textbf{B} \sin [2 \pi f\frac{r}{c}]$$
Thus
$$\frac{c}{\mu_0}\int_{V} \frac{1}{r^2} \frac{d}{dr}(r^2\textbf{B}^2 \sin^2 [2 \pi f\frac{r}{c}])4 \pi r^2 dr$$
Then we have a r dependency for the integral. I have tried and I ended up with a longer expression. The better news was that if I equated it with
$$\frac{c}{\mu_0}\textbf{B}^2 \frac{1}{2} T 4 \pi r^2$$
I ended up with an equation that only had R and f as variables since B is the same for the two divergence theorems versions from the derivations above. I guess I could initially determine R from a setup point of view. But unfortunately it did not give any solutions. It seems that since there are 2 Work equations. Equating thoose two could give a solution of frequency. But I have not found a solution that makes sense. Anyone that wants to try to find a solution for the frequency with this setup?
Here is my attempt attached just in case anyone want to take a look (the answer gave me 0 answers as far as I could tell):