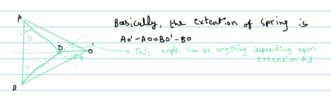Frequency of oscillations given 3 springs at angles ##\frac{2\pi}{3}##

[curious_mind]

Homework Statement

Block of mass #m# is attached to 3 springs of equal spring constants $k$. Angle between the springs are $\frac{\pi}{3}$ with Block at its center. If the Block is pushed against vertical wall and released, find the frequency of oscillation.

Relevant Equations

Probably there is no need to assume small oscillations.

$\omega = \sqrt{\dfrac{k}{m}}$

I am attaching the solution given, but I am not convinced with the approach. I am also asking for some suggestions and hints if I am wrong or is there any other way around.

The thing I do not understand is the arguments from geometry they have made. How they can conclude the extension of spring is $\sin \dfrac{2\pi}{3}$ because the projection they have drawn can subtend angle any other than $\dfrac{\pi}{2}$. To demonstrate this, I am also attaching a hand-drawn picture. I gave several thoughts on this problem, but not sure what to do.

Please show me some general method to approach such a problem. Thank you.

 

[Lnewqban]

This part is confusing: "If the particle is pushed against horizontal wall".
Also, can the springs work the same in tension and compression, or they can only be stretched?

 

[curious_mind]

Oh, sorry.. it is "Block is pushed against vertical wall" Three spring are configured in Y shaped. In the hand written diagram, I drawn horizontally, that is why confusing. Sorry and Thank you for pointing it out.

I hope it is clear. Editing now.

 

[haruspex]

the projection they have drawn can subtend angle any other than

The question ought to state that is for small perturbations x.
However, you might care to challenge the solution for another reason. Consider the case where the angle is zero instead of 60°.
Also, I assume the solution should read "the corresponding elongation in a and b".

 

[curious_mind]

Even in the small oscillations how the elongation would be $\sin \frac{\pi}{3}$. The projection of spring A to spring B need not to be perpendicular ? Right ?!

 

[haruspex]

Even in the small oscillations how the elongation would be $\sin \frac{\pi}{3}$. The projection of spring A to spring B need not to be perpendicular ? Right ?!

It is not a question of the projection of one spring on the other; it is the projection of the vertical displacement x on the springs. (And as I hinted, $\sin(\pi/3)$ is wrong.)

If you have trouble seeing that, try this:
Let the horizontal distance from the top of A to the centre line be H.
When the spring is at $\theta+\Delta\theta$ to the vertical, the length of the spring is $H\csc(\theta+\Delta\theta)$, so its extension is $H\csc(\theta+\Delta\theta)-H\csc(\theta)\approx-H\frac{\cos(\theta)}{\sin^2(\theta)}\Delta\theta$.
Meanwhile, the vertically downward displacement of the particle is $H\cot(\theta+\Delta\theta)-H\cot(\theta)\approx-H\frac{1}{\sin^2(\theta)}\Delta\theta$.
What is the ratio of the two?

 

[Lnewqban]

 

[curious_mind]

If you have trouble seeing that, try this:
Let the horizontal distance from the top of A to the centre line be H.
When the spring is at $\theta+\Delta\theta$ to the vertical, the length of the spring is $H\csc(\theta+\Delta\theta)$, so its extension is $H\csc(\theta+\Delta\theta)-H\csc(\theta)\approx-H\frac{\cos(\theta)}{\sin^2(\theta)}\Delta\theta$.

Yes, I have tried the same way. But in case of elongation of center spring C, do not we require distance $H+ \Delta H$ ?
And so, length of elongated spring A or B will be $( H+\Delta H)\csc(\theta + \Delta \theta)$?

 

[curious_mind]

View attachment 337063

Thanks for the diagram but Can you explain what you want to say ?

 

[haruspex]

Yes, I have tried the same way. But in case of elongation of center spring C, do not we require distance $H+ \Delta H$ ?
And so, length of elongated spring A or B will be $( H+\Delta H)\csc(\theta + \Delta \theta)$?

You seem to have misunderstood how I defined H. It is constant.

 

[curious_mind]

It is not a question of the projection of one spring on the other; it is the projection of the vertical displacement x on the springs. (And as I hinted, $\sin(\pi/3)$ is wrong.)

If you have trouble seeing that, try this:
Let the horizontal distance from the top of A to the centre line be H.
When the spring is at $\theta+\Delta\theta$ to the vertical, the length of the spring is $H\csc(\theta+\Delta\theta)$, so its extension is $H\csc(\theta+\Delta\theta)-H\csc(\theta)\approx-H\frac{\cos(\theta)}{\sin^2(\theta)}\Delta\theta$.
Meanwhile, the vertically downward displacement of the particle is $H\cot(\theta+\Delta\theta)-H\cot(\theta)\approx-H\frac{1}{\sin^2(\theta)}\Delta\theta$.
What is the ratio of the two?

So, the ratio of these two would be Vertical displacement is to length of spring which is equal to $\cos \theta$ is that you want to say ?

Which would mean if elongation is $\Delta l$ and vertical displacement is $x$, then for very small $x$, it would be $cos \theta = \dfrac{x}{\Delta l}$ which would imply $x = \Delta l \cos \theta$. But, Well well, in solution it is given that elongation $\Delta l = x \cos \theta$.
Correct ? Or am I misunderstanding anything?

 

[Lnewqban]

Thanks for the diagram but Can you explain what you want to say ?

I wanted to clarify my view of the initial condition, assuming certain equal pre-tension in each spring, holding the block in static balance of x and y forces.

Is the diagram and my understanding correct?

Again, can the springs work the same stretched and compressed?

Should we assume that the deflection and oscillation is to be limited to the x-axis by some horizontal guide?

 

[curious_mind]

Is the diagram and my understanding correct?

Diagram is correct.

can the springs work the same stretched and compressed?

Yes. I think the problem is symmetrical in this regard.

Should we assume that the deflection and oscillation is to be limited to the x-axis by some horizontal guide?

Not really, I think. Springs deflect in both horizontal and vertical components. Only Vertical spring oscillates in vertical component. I assume you are considering x-axis to be horizontal. I am not sure how you think oscillation is limited to horizontal direction, or am I misunderstanding what you say ? What you mean by "horizontal guide" ?

 

[Lnewqban]

... Only Vertical spring oscillates in vertical component.

Then, I don’t understand the movement.
Sorry, I am unable to help without creating confusion.

I assume you are considering x-axis to be horizontal. I am not sure how you think oscillation is limited to horizontal direction, or am I misunderstanding what you say ? What you mean by "horizontal guide" ?

Until now, I believed that the disturbance and following oscillation would have a horizontal direction.

 

[curious_mind]

Then, I don’t understand the movement.
Sorry, I am unable to help without creating confusion.

Until now, I believed that the disturbance and following oscillation would have a horizontal direction.

Well, I have to clarify I am talking with respect to first type written diagram.

In the typewritten solution, oscillation happens in the vertical direction.

In hand written illustration, oscillation happens in horizontal diagram.

It is just that I found caveats in vertical typewritten solution, so I tried to reproduce that.. but I drawn the same thing horizontally. This is why creating confusion. I am very sorry for this, but I hope now it is clear.

I think you are considering second hand written diagram.

 

[haruspex]

Which would mean if elongation is $\Delta l$ and vertical displacement is $x$, then for very small $x$, it would be $cos \theta = \dfrac{x}{\Delta l}$ which would imply $x = \Delta l \cos \theta$.

No, you have it backwards. The equations I posted lead to $\Delta l=x\cos(\theta)$.
The equation in post #1 has $\Delta l=x\sin(\theta)$, hence my second paragraph in post #4.

 

[curious_mind]

No, you have it backwards. The equations I posted lead to $\Delta l=x\cos(\theta)$.
The equation in post #1 has $\Delta l=x\sin(\theta)$, hence my second paragraph in post #4.

I see, I think I understood now your argument. Thank you.