TRB8985
- 74
- 15
- Homework Statement
- A 5.00 m, 0.732 kg wire is used to support two uniform 235 N posts of equal length. Assume that the wire is essentially horizontal and that the speed of sound is 344 m/s. A strong wind is blowing, causing the wire to vibrate in its 5th overtone. What are the frequency and wavelength this wire produces?
(Theta = 57.0°)
- Relevant Equations
- f_n = n * v/2L ; v = sqrt(F/mu) ; v_sound = f_n * lambda_sound
Good morning,
I'm working through the problem from the homework statement above and answered it correctly, but I can't help but feel that something important is missing.
I was able to correctly identify the sum of torques by using the following diagram, where the CCW rotational direction represents a positive torque:
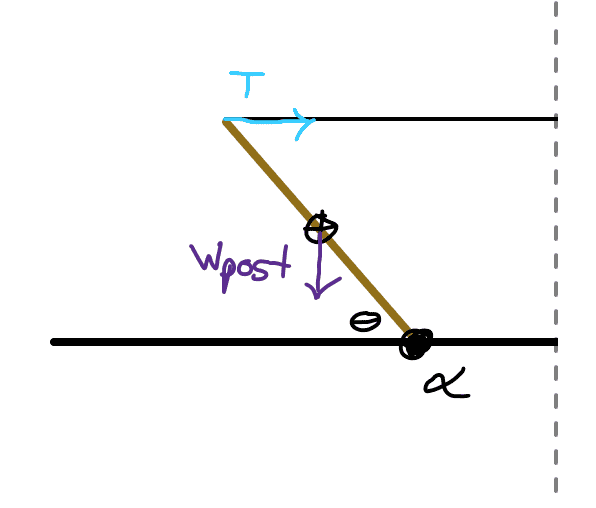
Equating the torque due to the weight of the post and the torque due to the tension (relative to point alpha) looks like this:
$$ W_{post} \cdot \frac {l}{2} cos(\theta) = T \cdot l sin(\theta) $$
This works out great, since the unknown length of the post (which I'm calling ##l##) cancels out and the tension can be used to solve the problem and get the right answer.
However, shouldn't we technically be including an additional torque due to the weight of the wire? Like this?
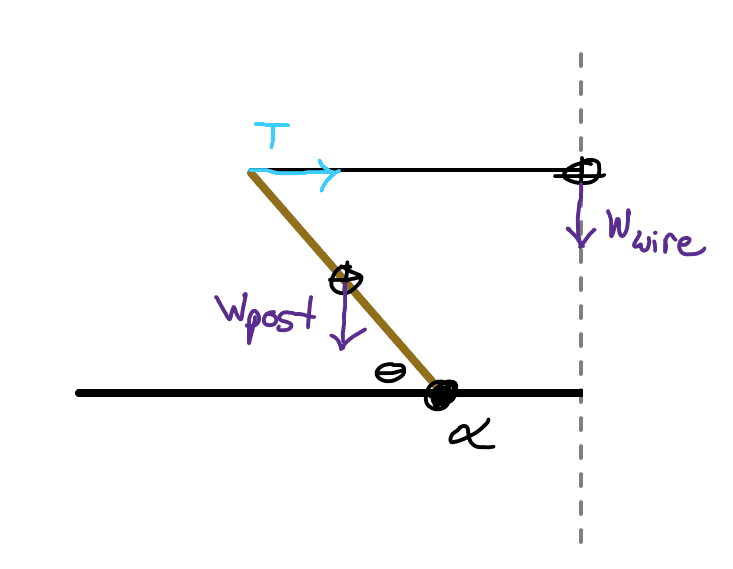
I wanted to try this and see what happens, but there's no obvious way to equate the torques which cancels out the length of the post like before:
$$ W_{post} \cdot \frac {l}{2} cos(\theta) = T \cdot l sin(\theta) + W_{wire} \cdot (2.50 m - l cos(\theta)) $$ It's possible to use geometry and determine the internal angles of this isoceles trapezoid figure, but that's not enough information to write the horizontal difference between ##\alpha## and the dashed line in terms of the post's unknown length.
It seems the only option is to just ignore the torque of the wire's weight and hand-wave it away as negligible compared to the other two forces, but that feels rather arbitrary.. is there a better way in the math to handle this situation?
Thank you!
I'm working through the problem from the homework statement above and answered it correctly, but I can't help but feel that something important is missing.
I was able to correctly identify the sum of torques by using the following diagram, where the CCW rotational direction represents a positive torque:
Equating the torque due to the weight of the post and the torque due to the tension (relative to point alpha) looks like this:
$$ W_{post} \cdot \frac {l}{2} cos(\theta) = T \cdot l sin(\theta) $$
This works out great, since the unknown length of the post (which I'm calling ##l##) cancels out and the tension can be used to solve the problem and get the right answer.
However, shouldn't we technically be including an additional torque due to the weight of the wire? Like this?
I wanted to try this and see what happens, but there's no obvious way to equate the torques which cancels out the length of the post like before:
$$ W_{post} \cdot \frac {l}{2} cos(\theta) = T \cdot l sin(\theta) + W_{wire} \cdot (2.50 m - l cos(\theta)) $$ It's possible to use geometry and determine the internal angles of this isoceles trapezoid figure, but that's not enough information to write the horizontal difference between ##\alpha## and the dashed line in terms of the post's unknown length.
It seems the only option is to just ignore the torque of the wire's weight and hand-wave it away as negligible compared to the other two forces, but that feels rather arbitrary.. is there a better way in the math to handle this situation?
Thank you!
Last edited: