Friction - problem with one of the equilibrium equations

[FEAnalyst]

Homework Statement

Calculate the minimum force for the system to stay in equilibrium (image attached).

Relevant Equations

sliding friction force

Hi,

actually it's not my homework, I'm just practicing some academic problems after a long break but it seems that I should post this here anyway. Here's a scheme of the problem that I want to solve:

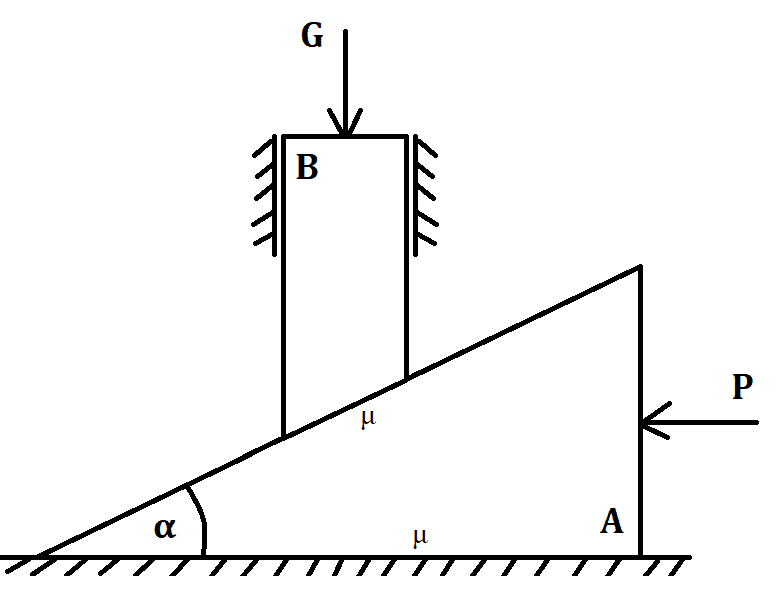
The task is to calculate minimum force $P$ for the system to stay in equilibrium.

And here's the FBD I made:

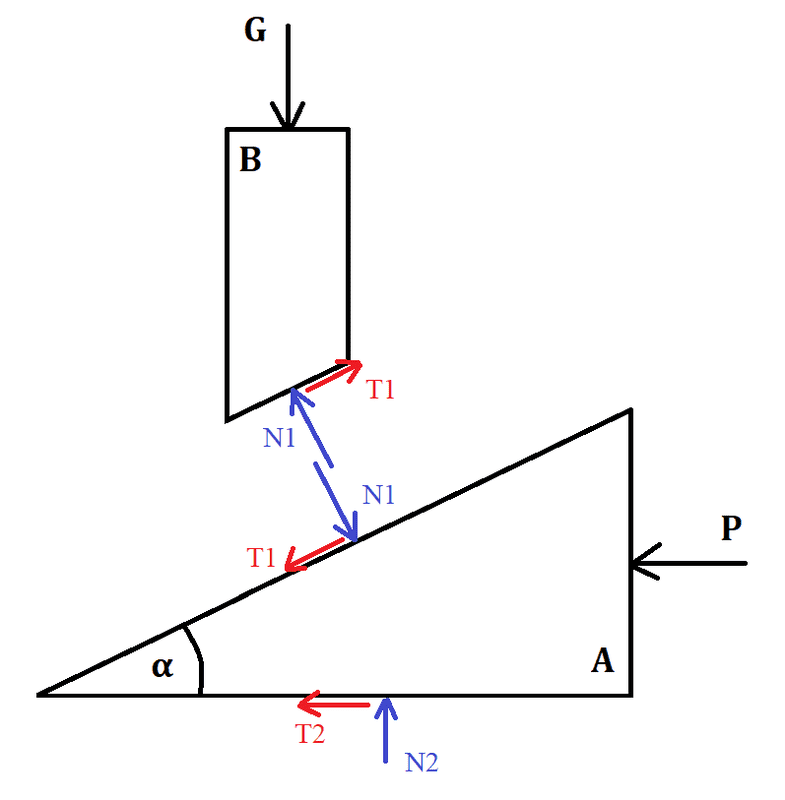
Normal (pressure) forces in blue, tangential (friction) forces in red, $\mu$ stands for friction coefficient here.

I wrote down the equilibrium equations and I could get the correct answer but only if I don't use the first equation - sum of forces in horizontal axis for body B: $$\sum Fx=0$$ $$T_{1} \cos(\alpha)-N_{1} \sin(\alpha)=0$$
It looks correct but if I substitute force values obtained from other equations then the result from this equation is completely wrong. Is the equation incorrect ? Or maybe my FBD is bad ?

I was thinking that it might be necessary to include normal forces acting on body B from guide (no friction there) but I'm not sure if that causes the problem.

Thanks in advance for your help.

 

[Arjan82]

Body B is clamped in the guide in x-direction. It is indeed possible it provides a reaction force, probably the guide is drawn for a reason ;).

But I don't think this is a very interesting balance? It doesn't add anything to answer the question for which force this system's equilibrium. Since horizontally body B isn't going anywhere.

 

[FEAnalyst]

That's right, but what may cause this problem with first equilibrium equation for body B then ?

 

[Steve4Physics]

$$T_{1} \cos(\alpha)-N_{1} \sin(\alpha)=0$$It looks correct but if I substitute force values obtained from other equations then the result from this equation is completely wrong. Is the equation incorrect ? Or maybe my FBD is bad ?

The horizontal normal force of the guide on B is missing (on the FBD and in the equation). And you need the FBD for wedge A if you don't already have it.

I'd write down the equilibrium equations for the vertical and horizontal forces acting on A. And for the vertical forces acting on B. Then see if a bit of algebra can yield P.

Incidentally:
- you are assuming A and B are weightless;
- 'brake should be 'break'!

 

[FEAnalyst]

I already have all the equilibrium equations. I can include the normal forces acting on B from the guide but they will cancel out anyway, right ? The assumption of weightless bodies is made in the book where I've found this example so I'll stick to it.

Here are the equations (all of them):
- body B: $$T_1 \cos{\alpha}-N_1 \sin{\alpha}+N-N$$ $$-G+T_1 \sin{\alpha}+N_1 \cos{\alpha}=0$$
- body A: $$-T_2 - P-T_1 \cos{\alpha} + N_1 \sin{\alpha}$$ $$N_2-T_1 \sin{\alpha}-N_1 \cos{\alpha}=0$$
- additional equations for friction: $$T_1=\mu N_1$$ $$T_2=\mu N_2$$
where: $N$ - aforementioned missing normal force. The rest is named as before.

As I've said before, when I substitute values for $G$, $\mu$ and $\alpha$ given in the book, I get the correct value of $P$. As long as I don't use the first equation.

Can you see any error here ?

 

[haruspex]

I can include the normal forces acting on B from the guide but they will cancel out anyway, right ?

No, what makes you think there are equal and opposite forces from the two sides?
If we ignore the friction between the two bodies for the moment, there is a net horizontal force on B and a net clockwise torque. So simplifying the guide's forces to two points, there is a force from the left and a weaker, higher force from the right.

How it works with the friction is less clear.

 

[Steve4Physics]

I already have all the equilibrium equations. I can include the normal forces acting on B from the guide but they will cancel out anyway, right ?

.
.

Can you see any error here ?

You can’t assume the normal forces from the guide on B will cancel out. The forces exerted on the different sides of B are (in general) asymmetric.

One way to understand this is to consider the situation with μ=0 (or μ = extremely small) so that frictional forces are negligible. In this case, for equilibrium:

For A: resolving horizontally: $P = N_1 sinα$
For B: resolving horizontally: $N_G = N_1 sinα$
where $N_G$ s the total horizontal force exerted by the guide on B.

In this (no friction) equilibrium situation, the guide would exert a force $N_G$ to the right on B, keeping B is in equilibrium.

If $N_L$ and $N_R$ are the normal reaction forces exerted by the left and right side of the guide, then $N_L – N_R = N_G$.

Does that make sense? I didn’t check your working beyond that.

Also, apologies for saying you need the FBD for wedge A when you already had one!

Edit: @haruspex beat me to it! Plus typo's corected.

 

[FEAnalyst]

It seems that the problem will become quite complex if we include these normal forces from the guide acting on body B. I think that author’s intention was to ignore these forces, just like tangential (friction) ones. What in such case ? Are my equations correct or is something wrong with them ? As I said before, I get the correct answer (same as the one in the book) and the only problem is that I can’t get the first equation right.

 

[Steve4Physics]

As I've said before, when I substitute values for $G$, $\mu$ and $\alpha$ given in the book, I get the correct value of $P$. As long as I don't use the first equation.

But the first equation is wrong (see previous posts). So using it is guaranteed to give an incorrect answer! Fortunately, the problem can be solved without using first equation.

 

[FEAnalyst]

Ok, so the first equation should be: $$T_1 \cos{\alpha}- N_1 \sin{\alpha}+N_G=0$$
and thus: $$T_1 \cos{\alpha}- N_1 \sin{\alpha}+N_L-N_R=0$$
right ?

But is it even solvable (assuming non-zero friction, like it should be done here) ? It seems that there are too many variables and too few equations now.

 

[Steve4Physics]

Ok, so the first equation should be: $$T_1 \cos{\alpha}- N_1 \sin{\alpha}+N_G=0$$
and thus: $$T_1 \cos{\alpha}- N_1 \sin{\alpha}+N_L-N_R=0$$
right ?

But is it even solvable (assuming non-zero friction, like it should be done here) ? It seems that there are too many variables and too few equations now.

There is no point whatsover in considering the separate forces $N_L$ and $N_R$. There is no way to find them because they depend, in part, on how tightly B fits into the guide. I only introduced them to help explain why the reaction of the guide on B is not zero. Their individual values are totally irrelevant.

If you wanted $N_G$ for some obscure reason, you could use the 2nd, 3rd and 4th equations to find $T_1$ and $N_1$. Then use the (corrected) 1st equation to find $N_G$. But the question does not ask you to do this, so there is no need to even consider it!

 

[FEAnalyst]

Thanks, I get it now. One more thing to make sure that I understand it correctly - is it right that if we ignore $N_G$, as it's apparently done in the book, then the first equation will have to be incorrect, we won't be able to use it and there will be no way to make it correct (other than including $N_G$) ?

 

[Steve4Physics]

Thanks, I get it now. One more thing to make sure that I understand it correctly - is it right that if we ignore $N_G$, as it's apparently done in the book, then the first equation will have to be incorrect, we won't be able to use it and there will be no way to make it correct (other than including $N_G$) ?

Yes, that's correct.

The problem is solved using the 2nd, 3rd and 4th equations (+ the equations for friction in terms of normal reactions).

The 1st equation is not used to solve the problem. So an incorrect 1st equation makes no difference the answer.

And the incorrect 1st equation can't be used for some other purpose as (without $N_G$) it is wrong. (However, there may be some situations where $N_G=0$, in which case the incorrect 1st equation would become correct by accident!)

 

[FEAnalyst]

Thank you very much for help. This example is more unusual than it seems at first. Too bad it wasn’t explained in the book and its author gave the final answer only.