A From Nyquist plot to real conductivity spectra (sigma)

AI Thread Summary
To convert a Nyquist plot into a real conductivity vs. frequency plot, one must derive the real part of the complex conductivity from the impedance data. The discussion highlights the need for clarity on whether the imaginary part is necessary for this transformation. Users share their methods for calculating real conductivity, emphasizing the importance of correct formulas for admittance. The original poster seeks guidance on ensuring their calculations are accurate. The conversation centers on the mathematical relationships between impedance, admittance, and conductivity.
Olha
Messages
2
Reaction score
0
TL;DR Summary
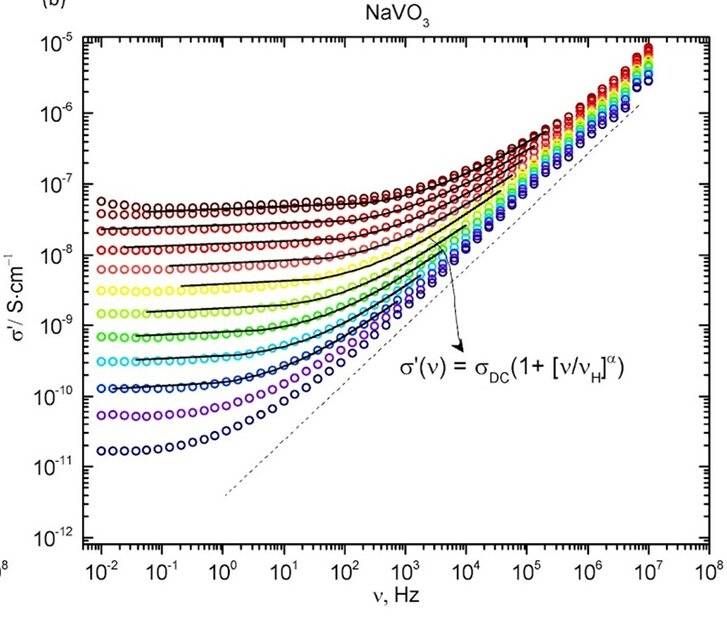
From Nyquist plot to real conductivity spectra (sigma) vs frequency
Hi, I have data of impedance but due to limitation of software after measurement I do not receive numerical values for admittance and real conductivity vs frequency. How mathematically I can convert Nyquist plot into plot real conductivity vs frequency?
conductivity spectra.jpg
 
Physics news on Phys.org
Your plot already shows the real part of the complex conductivity. Do you need the imaginary part?
 
Reply
  • Like
Likes Lord Jestocost
The image is the result I want to get. For now I have Nyquist plot Im vs Re, which I would like to transform it to the plot you see attached, real part of complex conductivity vs frequency. I have done it trough admittance but I am not sure in all formulas I used for it...
 
Please, show us your method.
 

Thread 'Need help understanding particle physics and quantum physics'

So I know that electrons are fundamental, there's no 'material' that makes them up, it's like talking about a colour itself rather than a car or a flower. Now protons and neutrons and quarks and whatever other stuff is there fundamentally, I want someone to kind of teach me these, I have a lot of questions that books might not give the answer in the way I understand. Thanks
View full post »

Similar threads

A AC transport data query (using a PPMS system)
Replies
3
Views
1K
Calculation of electrical mean free path in nanomaterials?
Replies
0
Views
3K
How to calculate complex permittivity from complex conductivity
Replies
4
Views
6K
Nyquist Plot Intersection with Real Axes
Replies
2
Views
6K
Philosophy of Science: Discussing Maths, Physics, Mind, & AI
Replies
3
Views
3K
Extracting Useful Information from Impedances
Replies
3
Views
2K
Calculate superconductor's magnetic susceptibility from Inductance
Replies
1
Views
2K
A Understanding MASERs and their properties
Replies
1
Views
2K
Trying to determine the Safe properties of Face Guards
Replies
13
Views
3K
Calculating Connector Impedance & Irregular Wire Char. Impedance
Replies
3
Views
3K

Hot Threads

Recent Insights

Back
Top