Fulcrum point loads

[rodgthedodge]

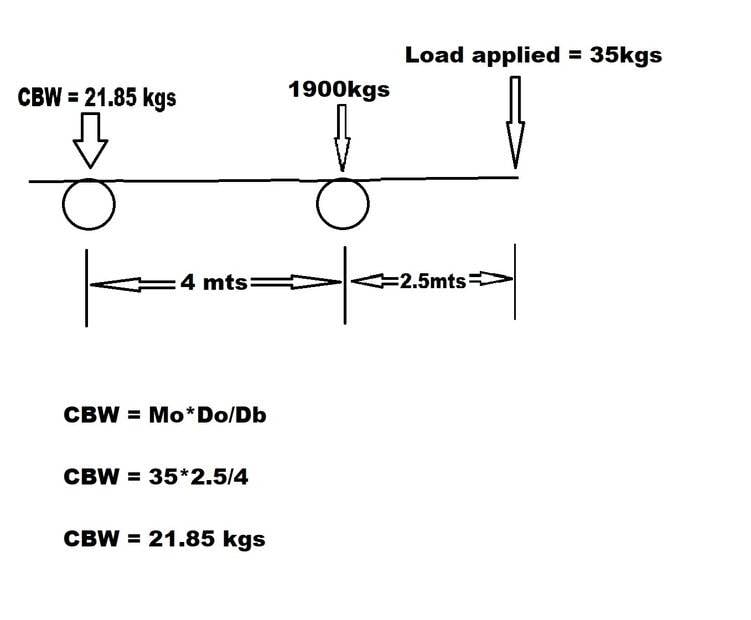
I have a motorhome and I want to calculate the extra weight I am applying to my rear axle by adding my ebike to the rear carrier. I have searched and found a counterbalance formula (added in the image) my question is do I just add the CBW to the fulcrum point. i.e rear axle weight calculation = 1900kgs +35kgs+21.85kgs new rear axle weight = 1956kgs, confused? confused.

 

[Baluncore]

Welcome to PF.

Adding the 35 kg ebike to the rear will add more than 35 kg to the rear axle.
It will also reduce the weight on the front axle by less than 35 kg.

What are the axle weights now ?

 

[Lnewqban]

Welcome, @rodgthedodge !
Can you add the counterweight further forward?
Any way to improve the rear suspension?

 

[jrmichler]

I have a motorhome and I want to calculate the extra weight I am applying to my rear axle by adding my ebike to the rear carrier.

Your calculation is correct, but confusing. Since you only want to calculate the extra weight from the ebike, you can ignore the weight of the motorhome. We do this by summing moments. A moment is a force multiplied by the distance from that force to a point. We can put that point where we want, so we choose that point so as to make the calculation as easy as possible. Since we want to find the extra weight on the rear wheels, that point will be the front wheels. The free body diagram then looks as follows:

The moment for the ebike is 6.5 m X 35 kg = 227.5 kg-m. The rear wheel load is unknown, but shown in the opposite direction, so we name it F, and the moment is 4 m X F = 4F kg-m. The sum of moments equals zero, so 227.5 - 4F = 0. Solve for F, and F = 227.5 / 4 = 56.875 kg. Round to the nearest kg, and the additional load is 57 kg. You can add that to the weight on the rear wheels to get the total weight on the rear wheels with the ebike.