Function Waves Graph Homework: Find λ for tp=3.5s and xp=3.7m

[negation]

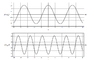
Homework Statement

The function y(x, t) = Asin(kx−ωt+ϕ) where x is in metres and t in seconds for
(a) t_p = 3.5 s and (b) x_p = 3.7m

The Attempt at a Solution

I don't even know where to begin.

I know λ = 2pi/k

this is really disorienting. In the first graph, I'm given t = 3.5.
A = 3
y(x,t) = 3sin(kx-3.5ω)

In the second graph, y(x,t) = 3sin(3.7k - ωt)

Really, I don't know how should I get started and I'm really frustrated.

I'm asked to find the wavelength. Is it 7m based off the first graph or do I have to utilize t = 3.5 and x=3.7?

 

[BvU]

Hello again,

Let's try to get you unfrustrated. The problem statement apparently includes a question like: what is the wavelength ? (because you mention it under 3). And it has something to do with k (because you include it under 3 -- but λ = 2pi/k looks more like a relevant equation to me than an attempt at solution -- Please make it easier for yourself and be a bit more complete under 1) and 2) ).

1.) I see an A = 3 falling out of the air. Where does it come from ?

2.) If the first plot is for a fixed t, the only thing that varies is x and you have a plot of A sin(kx + something). How would you find k and, thereby λ (according to relevant equation 1) ? Is this part of a longer exercise, or is the second plot there just to confuse you ?

 

[negation]

Hello again,

Let's try to get you unfrustrated. The problem statement apparently includes a question like: what is the wavelength ? (because you mention it under 3). And it has something to do with k (because you include it under 3 -- but λ = 2pi/k looks more like a relevant equation to me than an attempt at solution -- Please make it easier for yourself and be a bit more complete under 1) and 2) ).

1.) I see an A = 3 falling out of the air. Where does it come from ?

2.) If the first plot is for a fixed t, the only thing that varies is x and you have a plot of A sin(kx + something). How would you find k and, thereby λ (according to relevant equation 1) ?


Is this part of a longer exercise, or is the second plot there just to confuse you ?

Hi BVU,

I'm overlooking certain aspects in this question.

It's part of a longer question but I had it solved.

I am asked to find the wavelength given the 2 graph. The wavelength of a wave is simply taken to be the length of a wave per cycle.
In the first graph, the wavelength is 7m. This turns out to be correct. It starts at x =0 and ends at x=7.
What had me confused was the given t_p and x_p.