Fundamental matrix for complex linear DE system

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

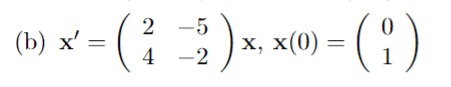
I am trying to find the fundamental matrix, however, the eigenvalues are both imaginary and so are the eigenvectors. That is, $\lambda_1 = 4i, \lambda_2 = -4i$

$v_1 = (1 + 2i, 2)^T$
$v_2 = (1 - 2i, 2)^T$

So I think I just have an imaginary matrix? This is because the general solution is $\vec x = c_1(1 + 2i, 2)^T e^{4it} + c_2(1 - 2i, 2)^T e^{-4it}$, then does someone please know whether I can just write the system in the form $\vec x = \vec Φ \vec c$ where $c = (c_1, c_2)^T$ and Φ is complex?

Thanks!

 

[nuuskur]

Why is it a problem that eigenvalues are not real? A fundamental matrix of the system is a matrix-valued function $\Phi$ such that the columns of $\Phi(t)$ are linearly independent solutions of the given system for all $t$. Simply write how $\Phi(t)$ is parametrised with respect to $t$ and you are done.

 

[FactChecker]

The algebra and analysis with complex values work at least as well as with real values. If you are familiar with the complex exponential function, you should be able to do the analysis.

 

[zenterix]

Here are a few things to note

- By finding an eigenvalue $\lambda_1$ and an associated eigenvector $\vec{v}_1$, you have found a complex solution of form $e^{\lambda_1 t}\vec{v_1}$.

- The other eigenvalue and eigenvector is another complex solution.

- If we are looking for two real solutions then it turns out that given one single complex solution, the real and imaginary parts are each a real solution. In addition, these two real solutions are linearly independent.

- Therefore, all you have to do is take one of the complex solutions, expand the terms and do algebra until you have a real and an imaginary part clearly separated. A little more detail on what this entails:

-- you will have something like $e^{zt}\vec{v}$ where $z\in\mathbb{C}$.

-- write $e^{zt}$ as a real exponential times an imaginary exponential (which you expand into sine and cosine using Euler's formula)

-- write the eigenvector $\vec{v}$ as the sum of a real vector and an imaginary vector

-- Now you can multiply everything so that you get a real part and an imaginary part for the expression as a whole.

- At that point, you have two real solutions which when placed as columns of a matrix makes this matrix a fundamental matrix.

 

[pasmith]

You know from the Cayley-Hamilton theorem that $A = \begin{pmatrix}2 & - 5 \\ 4 & - 2 \end{pmatrix}$ satisfies its own characteristic polynomial, so that $A^2 = -4^2I$. It follows that you can compute $\Phi(t) = \exp(At)$ directly: $$\begin{split} \exp(At) &= \sum_{n=0}^\infty \frac{A^{2n}t^{2n}}{(2n)!} + \sum_{n=0}^\infty \frac{A^{2n+1}t^{2n+1}}{(2n+1)!} \\ &= \sum_{n=0}^\infty \frac{(-1)^n4^{2n}t^{2n}}{(2n)!} + A \sum_{n=0}^\infty \frac{(-1)^n4^{2n}t^{2n+1}}{(2n+1)!} \\ &= I\cos 4t + \frac{\sin 4t}{4} A. \end{split}$$

Spoiler: General case for a 2D system

Indeed we can do this for any 2x2 matrix $A$, because we can write the characteristic polynomial in the form $$(A - bI)^2 = cI.$$ Since the relevant matrices commute we have $$e^{-bt}\exp(At) = \exp(-btI)\exp(At) = \exp(At)\exp(-btI) = \exp((A - bI)t)$$ and in the same manner as the above, $$\begin{split} \exp((A - bI)t) &= \sum_{n=0}^\infty \frac{c^nt^{2n}}{(2n)!}I + \sum_{n=0}^\infty \frac{c^{n}t^{2n+1}}{(2n+1)!}A \\ &= \begin{cases} \cosh(\sqrt{c}t)I + \frac{\sinh(\sqrt{c}t)}{\sqrt{c}}A & c \neq 0 \\ I + (A- bI)t & c = 0. \end{cases} \end{split}$$ Hence $$\exp(At) = \begin{cases} e^{bt}\cosh(\sqrt{c}t)I + \frac{e^{bt}\sinh(\sqrt{c}t)}{\sqrt{c}}A & c \neq 0 \\ (1 - bt)e^{bt}I + Ate^{bt} & c = 0.\end{cases}$$ Note also the identities $$\cosh(iz) = \cos z \qquad \sinh(iz) = i\sin z.$$