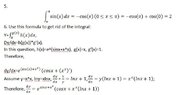Fundamental Theorem of Calculus Questions

In summary, the Fundamental Theorem of Calculus is a key concept in calculus that relates the derivative and integral of a function. It allows for easy calculation of derivatives and provides a fundamental connection between differentiation and integration. The theorem has two parts, one for closed intervals and one for open intervals, and is used in various real-life applications. However, it only applies to continuous functions with antiderivatives and cannot be used for improper integrals.
  • #1
akbarali
19
0
Last one for the night!

These are the questions: View attachment 792

This is my work: View attachment 793

I think question 5 is correct (I hope), but I'm not entirely sure about question 6. Any help would be appreciated!
 

Attachments

  • Fundamental1.jpg
    Fundamental1.jpg
    13.2 KB · Views: 70
  • Fundamental2.jpg
    Fundamental2.jpg
    29.1 KB · Views: 62
Physics news on Phys.org
  • #2
For the first one, I agree with your result. Good work! (Rock)

For the second one, the derivative form of the FTOC gives us:

If:

\(\displaystyle G(x)=\int_a^x f(t)\,dt\)

then:

\(\displaystyle G'(x)=f(x)\)

You have cited a more general case, but can you see that you have added something to your result which should not be there?
 
  • #3
Hmm, are you saying the answer should just be exp(sin(x)+ x^x) ?
 
  • #4
Yes, your formula doesn't have $h'(x)$ in it, right?
 
  • #5
Is there any way you would work these problems differently from how I did that would help me better solve such problems in the future?
 
  • #6
The first problem I would write:

\(\displaystyle \int_0^{\pi}\sin(x)\,dx=-\left[\cos(x) \right]_0^{\pi}=-\left(\cos(\pi)-\cos(0) \right)=-(-1-1)=-(-2)=2\)

For the second problem, I would simply write:

\(\displaystyle \frac{d}{dx}\left(\int_0^x e^{\sin(s)+s^s}\,ds \right)=e^{\sin(x)+x^x}\)
 
  • #7
You have been helping me all night. So grateful for your work. I have two more problems that are bugging the heck out of me, but I think I should let you rest for the night! Hehe
 

FAQ: Fundamental Theorem of Calculus Questions

What is the Fundamental Theorem of Calculus?

The Fundamental Theorem of Calculus is a fundamental concept in calculus that connects two important concepts: the derivative and the integral. It states that the derivative of a function can be found by evaluating its antiderivative at a specific point.

Why is the Fundamental Theorem of Calculus important?

The Fundamental Theorem of Calculus is important because it allows us to easily calculate the derivative of a function without having to use the limit definition. It also provides a fundamental connection between the concepts of differentiation and integration, making it a key concept in understanding calculus.

What are the two parts of the Fundamental Theorem of Calculus?

The first part of the Fundamental Theorem of Calculus states that if a function is continuous on a closed interval, then the area under its curve can be found by evaluating its antiderivative at the endpoints of the interval. The second part states that if a function is continuous on an open interval, then the derivative of its integral is equal to the original function.

How is the Fundamental Theorem of Calculus used in real-life applications?

The Fundamental Theorem of Calculus is used in a wide range of real-life applications, such as physics, engineering, economics, and statistics. It is used to solve optimization problems, calculate areas and volumes, and model rates of change in natural phenomena.

Are there any limitations to the Fundamental Theorem of Calculus?

While the Fundamental Theorem of Calculus is a powerful tool in calculus, it does have some limitations. It only applies to continuous functions, and it assumes that the function has an antiderivative. It also cannot be used to evaluate improper integrals, which have infinite or undefined limits of integration.

Similar threads

B Question about the fundamental theorem of calculus
Replies
2
Views
1K
B A proof of the fundamental theorem of calculus
Replies
6
Views
2K
MHB Fundamental theorem of calculus and more....
Replies
9
Views
2K
I Questions about the fundamental thoerem of calculus
Replies
10
Views
2K
B Some help understanding integrals and calculus in general
2
Replies
42
Views
4K
I Visual interpretation of Fundamental Theorem of Calculus
Replies
5
Views
2K
Fundamental theorem of calculus for double integral
Replies
1
Views
1K
I Can Schwarz's Theorem be used "Backwards" to prove continuity?
Replies
21
Views
1K
First Fundamental Theorem of Calculus
Replies
15
Views
2K
Why is ##g## differentiable only on ##(a,b)## and not on ##[a,b]##?
Replies
12
Views
2K

Hot Threads

Recent Insights

Back
Top