- #1
Galilean form of the law of transformation of velocities
- Thread starter user5
- Start date
-
- Tags
- Form Galilean Law Transformation
In summary, the conversation involved finding the angle of a motorist's velocity with respect to the line of sight of a police car. At first, there was confusion about what was meant by "line of sight" but it was clarified to be the direction in which the police car was moving. The final answer was 15°, but there was some discussion about signs and drawing diagrams to accurately represent the angles. The conversation ended with the expert suggesting to draw the line of sight and the velocity vector on the same diagram to find the angle between them.
- #2
Doc Al
Mentor
- 45,588
- 2,312
By "line of sight" they mean the direction in which the police car is moving. (Where they would be looking straight ahead.) So imagine an axis extending forward from the police car.user5 said:
To find the angle, figure out the velocity of the motorist in the frame of the police car.
- #3
user5
- 38
- 0
I get -39°...not 15°...
Last edited:
- #4
Doc Al
Mentor
- 45,588
- 2,312
Show how you got that.user5 said:
- #5
user5
- 38
- 0
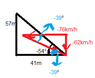
α=arctan(-62/76)
- #6
Doc Al
Mentor
- 45,588
- 2,312
Ah, I was wrong about what they meant by "line of sight". Line of sight is the line directed from the police car to the motorist. Find the angle with respect to that line and you'll get the answer given.user5 said:
- #7
user5
- 38
- 0
I'm confused, now I got -54° and what does the minus sign mean in that situation, may you give some more details about the solution...
- #8
Doc Al
Mentor
- 45,588
- 2,312
Don't worry about signs. Instead, draw yourself a picture. Show the line of sight (which is based on distances) and then add the direction of the velocity, which you already found. Find the angle between those two.user5 said:
- #9
user5
- 38
- 0
Are signs meaningless?
- #10
Doc Al
Mentor
- 45,588
- 2,312
No, but rather than rely on the mechanical use of a formula you would be better off simply drawing the relevant angles. Then you wouldn't have questions about signs.user5 said:
- #11
- #12
Doc Al
Mentor
- 45,588
- 2,312
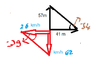
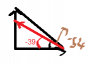
The first diagram is drawn correctly: The hypotenuse represents the line of sight.user5 said:
The second diagram needs to be redrawn to represent the sum of those velocity vectors. That vector will represent the relative velocity.
- #13
user5
- 38
- 0
76 need to be reversed ...How do those drawings show me that I need to subtract those angles?
Last edited:
- #14
Doc Al
Mentor
- 45,588
- 2,312
When adding vectors graphically you must have the tail of one start at the head of the other.user5 said:
You want the angle that the velocity makes with the line of sight. Draw them both on the same diagram and find the angle between them.
- #15
- #16
Doc Al
Mentor
- 45,588
- 2,312
(1) We are just comparing directions; dimensions are irrelevant.user5 said:
(2) Your diagram is still not right. You want: tail - head - tail - head. You have: head - tail - tail - head.
(3) Find the angle each direction vector makes with the horizontal; then you can find the angle they make with each other by subtracting.
- #17
- #18
Doc Al
Mentor
- 45,588
- 2,312
It's not a question of rotating the triangle, but drawing it correctly. Note that the velocity vector will point towards the police car.user5 said:
Yes, but don't worry about the minus sign. I'm sure they just want the magnitude.
You are most welcome.
- #19
user5
- 38
- 0
Sorry for asking again...Do you mean that velocity vector of 76 points toward the police while motorist have a velocity vector towards him of 62?
Last edited:
- #20
Doc Al
Mentor
- 45,588
- 2,312
The velocity vector of the motorist with respect to the Police will point somewhat towards the Police. Not exactly of course--it will make an angle of 15° to the line of sight. In your diagram in post #17 the red arrow, which I presume represents the velocity of the motorist with respect to the police, points in the wrong direction.user5 said:
- #21
- #22
Doc Al
Mentor
- 45,588
- 2,312
It's hard to say from your diagram, but I think you have the correct angles for the line of sight and for the velocity.user5 said:
To see what's going on, do this. On the original diagram, the one that described the problem, draw a line from motorist to police. That's the line of sight. You already figured out the angle it makes with the horizontal.
Then, on that same diagram, draw the velocity vector (the velocity of the motorist relative to the police) emanating from the position of the motorist. You have already figured out the angle that that vector makes with the horizontal.
Then you'll be able to figure out the angle between those two lines, using a bit of geometry.
FAQ: Galilean form of the law of transformation of velocities
What is the Galilean form of the law of transformation of velocities?
The Galilean form of the law of transformation of velocities is a principle in classical mechanics that describes how velocities are transformed between two frames of reference that are moving at constant speeds relative to each other.
How does the Galilean form of the law of transformation of velocities differ from the relativistic form?
The Galilean form of the law of transformation of velocities is based on classical mechanics and assumes that time and space are absolute. In contrast, the relativistic form takes into account the effects of special relativity, which states that the laws of physics are the same for all observers in uniform motion.
What is the significance of the Galilean form of the law of transformation of velocities?
The Galilean form of the law of transformation of velocities is important in classical mechanics as it allows us to predict the motion of objects in different frames of reference. This is useful in many practical applications, such as calculating the trajectory of a projectile or the motion of a car.
Can the Galilean form of the law of transformation of velocities be applied to all situations?
No, the Galilean form of the law of transformation of velocities is only applicable in situations where the relative speeds between the frames of reference are much smaller than the speed of light. In cases where this is not true, the relativistic form of the law must be used instead.
How does the Galilean form of the law of transformation of velocities relate to other principles in classical mechanics?
The Galilean form of the law of transformation of velocities is closely related to the principle of inertia and the principle of relativity, both of which are fundamental principles in classical mechanics. These principles all work together to explain the motion of objects in different frames of reference.