Galois Theory - Structure Within Aut(K/Q) ....

[Math Amateur]

I am reading "Abstract Algebra: Structures and Applications" by Stephen Lovett ...

I am currently focused on Chapter 8: Galois Theory, Section 1: Automorphisms of Field Extensions ... ...

I need help with Example 11.1.10 on page 560 ... ...Example 11.1.10 reads as follows:

My questions regarding the above example are as follows:

Question 1In the above text from Lovett we read the following:

" ... ... It is easy to show that $\text{Aut} ( K / \mathbb{Q} ( \sqrt[3]{13} ) \ \cong \mathbb{Z}_2$ ... ... "Can someone please help me to show that $\text{Aut} ( K / \mathbb{Q} ( \sqrt[3]{13} ) \ \cong \mathbb{Z}_2$ ... ... ?

Question 2In the above text from Lovett we read the following:

" ... ... By Proposition 11.1.4, there are at most three options where to map $\sqrt[3]{13}$ and at most two options where to map $\sqrt{ -3 }$ ... ... "My question is ... what are the three options where to map $\sqrt[3]{13}$ ... surely there is only one option to map $\sqrt[3]{13}$ as the field extension is over $\mathbb{Q}$ and two of the "options" are imaginary or complex numbers ... or is Lovett just relying on "at most" ... why not rule out the complex roots straight away ... similarly I am puzzled about the two options for $\sqrt{ -3 }$ ... I am also puzzled about the role of Proposition 11.1.4 in this matter ... How does Proposition 11.1.4 ensure that there are at most three options where to map $\sqrt[3]{13}$ and at most two options where to map $\sqrt{ -3 }$ ... ... ... can someone please clarify the situation ...The above question refers to Proposition 11.1.4 ... ... so I am providing the text of that proposition ... ... as follows ... ...

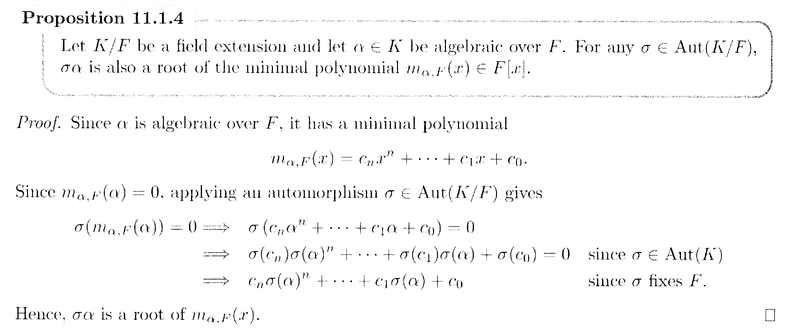
Help with the above questions will be much appreciated ... ...

Peter
***EDIT***

Just thinking ... since $K = \mathbb{Q} ( \sqrt[3]{13}, \sqrt{ -3 } )$ it already contains a complex number, namely $\sqrt{ -3 } = \sqrt{ 3 }i$ ... maybe that partly explains my questions ... ... and I think it is $K$containing the relevant roots, not $\mathbb{Q}$ as I was implying above ...

 

[fresh_42]

My questions regarding the above example are as follows:
Question 1
In the above text from Lovett we read the following:
" ... ... It is easy to show that $\text{Aut} ( K / \mathbb{Q} ( \sqrt[3]{13} ) \ \cong \mathbb{Z}_2$ ... ... "Can someone please help me to show that $\text{Aut} ( K / \mathbb{Q} ( \sqrt[3]{13} ) \ \cong \mathbb{Z}_2$ ... ... ?

Let us forget about $\sqrt[3]{13}$ for a moment and note $\mathbb{Q}[\sqrt[3]{13}] = F$. Then $K = F[\sqrt{-3}]$.
Which automorphisms $\operatorname{Aut}(K/F)$ of $K$ that keep $F$ fixed do you have here?

Question 2
In the above text from Lovett we read the following:
" ... ... By Proposition 11.1.4, there are at most three options where to map $\sqrt[3]{13}$ and at most two options where to map $\sqrt{ -3 }$ ... ... "My question is ... what are the three options where to map $\sqrt[3]{13}$ ... surely there is only one option to map $\sqrt[3]{13}$ as the field extension is over $\mathbb{Q}$ and two of the "options" are imaginary or complex numbers ... or is Lovett just relying on "at most" ... why not rule out the complex roots straight away ... similarly I am puzzled about the two options for $\sqrt{ -3 }$ ... I am also puzzled about the role of Proposition 11.1.4 in this matter ... How does Proposition 11.1.4 ensure that there are at most three options where to map $\sqrt[3]{13}$ and at most two options where to map $\sqrt{ -3 }$ ... ... ... can someone please clarify the situation ...

Have you calculated the minimal polynomial of $\mathbb{Q} \subseteq \mathbb{Q}(\sqrt[3]{13},\sqrt{-3})\,$? It has three possible roots, $\sqrt[3]{13} \, , \, +\sqrt{-3}\, , \,-\sqrt{-3}\,$. It is only one polynomial and all those have to be roots.

 

[Math Amateur]

Let us forget about $\sqrt[3]{13}$ for a moment and note $\mathbb{Q}[\sqrt[3]{13}] = F$. Then $K = F[\sqrt{-3}]$.
Which automorphisms $\operatorname{Aut}(K/F)$ of $K$ that keep $F$ fixed do you have here?

Have you calculated the minimal polynomial of $\mathbb{Q} \subseteq \mathbb{Q}(\sqrt[3]{13},\sqrt{-3})\,$? It has three possible roots, $\sqrt[3]{13} \, , \, +\sqrt{-3}\, , \,-\sqrt{-3}\,$. It is only one polynomial and all those have to be roots.

Thanks for the help fresh_42 ... ...

You write:

"Let us forget about $\sqrt[3]{13}$ for a moment and note $\mathbb{Q}[\sqrt[3]{13}] = F$. Then $K = F[\sqrt{-3}]$.
Which automorphisms $\operatorname{Aut}(K/F)$ of $K$ that keep $F$ fixed do you have here?"I think the automorphisms $\operatorname{Aut}(K/F)$ of $K$ that keep $F$ fixed would be as follows:$\sigma ( \sqrt{ -3} ) = \sqrt{ -3}$ ... ... (identity)

and

$\tau ( \sqrt{ -3} ) = - \sqrt{ -3}$Is that correct?
You also write:

"Have you calculated the minimal polynomial of $\mathbb{Q} \subseteq \mathbb{Q}(\sqrt[3]{13},\sqrt{-3})\,$?"

Minimum polynomial is $m(x) = (x^3 - 13)( x^2 + 3)$

Is that correct?On the question of Lovett taking about the three options to map $\sqrt[3]{13}$ ... ... is it just that he uses the term "at most" ?

Peter

 

[fresh_42]

I think the automorphisms $\operatorname{Aut}(K/F)$ of $K$ that keep $F$ fixed would be as follows:
$\sigma ( \sqrt{ -3} ) = \sqrt{ -3}$ ... ... (identity)
and
$\tau ( \sqrt{ -3} ) = - \sqrt{ -3}$
Is that correct?

Yes.

You also write:
"Have you calculated the minimal polynomial of $\mathbb{Q} \subseteq \mathbb{Q}(\sqrt[3]{13},\sqrt{-3})\,$?"
Minimum polynomial is $m(x) = (x^3 - 13)( x^2 + 3)$
Is that correct?

I think so. In the end we have a tower $\mathbb{Q} \subseteq \mathbb{Q}(\sqrt{-3}) \subseteq \mathbb{Q}(\sqrt{-3},\sqrt[3]{13})$, i.e. an extension of degree two and one of degree three or vice versa.

On the question of Lovett taking about the three options to map $\sqrt[3]{13}$ ... ... is it just that he uses the term "at most" ?

I think I was thinking wrongly here. His upper bound of (at most, yes) three comes from the principle possibility to map $\sqrt[3]{13}$ onto itself and the other two (complex) roots of $x^3 - 13$. I haven't done the math but he mentions that $\mathbb{Q}(\sqrt{-3})$ contains the third roots of unity, and thus can be used to create the missing roots of $x^3-13$ if the real one $\sqrt[3]{13}$ is available.

 

[Math Amateur]

Yes.

I think so. In the end we have a tower $\mathbb{Q} \subseteq \mathbb{Q}(\sqrt{-3}) \subseteq \mathbb{Q}(\sqrt{-3},\sqrt[3]{13})$, i.e. an extension of degree two and one of degree three or vice versa.

I think I was thinking wrongly here. His upper bound of (at most, yes) three comes from the principle possibility to map $\sqrt[3]{13}$ onto itself and the other two (complex) roots of $x^3 - 13$. I haven't done the math but he mentions that $\mathbb{Q}(\sqrt{-3})$ contains the third roots of unity, and thus can be used to create the missing roots of $x^3-13$ if the real one $\sqrt[3]{13}$ is available.

Thanks fresh_42 ...

Still reflecting on what you have said and reading and re-reading the example ...

In particular wondering where the mapping $\sigma$ comes from ...?

Peter

 

[fresh_42]

In particular wondering where the mapping σσ \sigma comes from ...?

Good question! As I see it , $\sigma = \rho$. Haven't even noticed this error.

 

[Math Amateur]

Good question! As I see it , $\sigma = \rho$. Haven't even noticed this error.

Yes, agree ...

Thanks again for your help ...

Peter